Motor lowers a mass over a pulley, find acceleration of mass

[Nicoleeeeeee]

Homework Statement

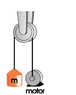
When the motor in the figure below lowers the m = 1200kg mass, it produces a tension of 1.15E+4N in the cable on the right side of the pulley. The pulley has a moment of inertia of 71.3kgm^2 and a radius of 0.794m. The cable rides over the pulley without slipping. Determine the acceleration of the m = 1200kg mass. Use g=9.81m/s^2.

Homework Equations

torque = I * alpha
torque = F*r
alpha = a/r[/B]

The Attempt at a Solution

T1=mg-ma

torque=(T1-T2)r

Ia/r=(T1-T2)r
Ia/r^2=mg-ma-T2
Ia/r^2+ma=mg-T2
a=(mg-T2)/(I/r^2 + m)
a=0.198m/s^2[/B]

This is the incorrect answer and the acceleration should be negative since it is going down. I don't know where I'm going wrong.

 

[kuruman]

Your derivation looks correct. When I put in the numbers, I got a slightly higher value than you. Redo the numbers without rounding off. I do mine on a spreadsheet. Maybe your answer was just outside the tolerance of the answer-checking algorithm.

Don't confuse acceleration with velocity. The fact that the velocity is negative does not necessarily mean that the acceleration is also negative. The speed may be decreasing while the mass is descending which means the acceleration is "up". However, here the acceleration is actually down. When you wrote the equation T1 - mg = -ma, the negative sign on the right side means "down" while symbol "a" stands for the magnitude of the acceleration, which you expect to come out positive when you substitute numbers. If it came out negative, then this would mean that you chose the direction incorrectly and the acceleration is actually "up".

 

[haruspex]

When I put in the numbers, I got a slightly higher value than you.

Same here, but it is not really meaningful. The calculation involves taking the difference of two numbers that only differ by a couple of percent. The consequence is that there is barely one digit of precision left. The answer could be ±20%.
Maybe that's the reason for the rejection. Try just 0.2, or -0.2.

 

[kuruman]

Try just 0.2, or -0.2.

I would try -0.2 first. Note that the question does not ask for the magnitude of the acceleration. If it is well-written, the scoring algorithm expects an answer that indicates knowledge of the vector nature of the acceleration.