Multiple resistors not in series / parallel

[trollcast]

Homework Statement

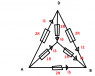
Circuit as shown: (sorry about the amazing paint skills)

The pd is being applied from A to B (C is in the centre of the circle)

(1) Determine the relations between the current by reversing V and using symmetry or by any other suitable method

(2) Calculate the total resistance across AB

(3) Determine the magnitudes of the currents in terms of V

(4) Redraw the circuit with CD as the base.
If the pd is now applied across CD determine the resistance across CD

(5) Redraw the circuit with AC as the base. Explain why the resistance across AC cannot be calculated in terms of resistances in series / parallel

Homework Equations

The Attempt at a Solution

(1) Using Kirchoffs Current Law

$$
I_1 + I_3 + I_5 = V/R_T \\

I_2 + I_4 + I_5 = V/R_T \\

I_3 + I_6 = I_4 \\

I_1 = I_2 + I_6 \\
$$

Using Kirchoffs Voltage Law

$$
-2I_1-2I_2+2I_5=0 \\
-2I_1-3I_6+I_3=0\\
-I_3-I_4+2I_5=0\\
3I_6-2I_2+I4=0\\
-I_4+2I_5-I_3=0\\
$$

(2) I can see that I can use the equations from (1) as simultaneous equations and therefore work out the resistance?

 

[Simon Bridge]

Did you try it and see?
7 unknowns and 9 equations certainly looks promising.

 

[gneill]

You can certainly attack the problem with KCL and KVL to arrive at a solution, but sometimes an appeal to symmetry can lead to a quicker and more elegant result.

Take a look at the 3R resistor. Suppose for a moment that it was removed from the circuit. How would the potential at D compare to the potential at C?

 

[trollcast]

You can certainly attack the problem with KCL and KVL to arrive at a solution, but sometimes an appeal to symmetry can lead to a quicker and more elegant result.

Take a look at the 3R resistor. Suppose for a moment that it was removed from the circuit. How would the potential at D compare to the potential at C?

Without the 3R resistor the potential at C and D would be the same as the pd from A to C to B is split between a 1R and 1R resistor.

The pd from A to D to B is again split between a 2R and 2R resistor so its half the pd?

 

[gneill]

Without the 3R resistor the potential at C and D would be the same as the pd from A to C to B is split between a 1R and 1R resistor.

The pd from A to D to B is again split between a 2R and 2R resistor so its half the pd?

Right. What does that tell you about the current through the 3R resistor? Does the 3R resistor have any effect on the circuit?

 

[trollcast]

Right. What does that tell you about the current through the 3R resistor? Does the 3R resistor have any effect on the circuit?

It must equal zero ?

So not all the currents indicated in that circuit are actually flowing then?

 

[gneill]

It must equal zero ?

Yup.

So not all the currents indicated in that circuit are actually flowing then?

Zero is a perfectly good number

If a current through a branch happens to be zero you can remove that branch. Or, equivalently, if two nodes have the same potential you can join them with a short circuit (direct wire) without affecting the circuit operation. So here you can either remove the 3R resistor or replace it with a wire. That should make things easier to analyze.

 

[quantum2013]

You can certainly attack the problem with KCL and KVL to arrive at a solution, but sometimes an appeal to symmetry can lead to a quicker and more elegant result.

Take a look at the 3R resistor. Suppose for a moment that it was removed from the circuit. How would the potential at D compare to the potential at C?

Could you please explain how symmetry would show a relation between the currents ?

for (3), would
i₂=i₁=\frac{V}{4}
i₃=i₄=\frac{V}{2}
be the correct answer to (3)?

 

[gneill]

Could you please explain how symmetry would show a relation between the currents ?

for (3) would
i₂=i₁=\frac{V}{4}
i₃=i₄=\frac{V}{2}
be the correct answer to the (3)?

That's the idea, although technically you should include the R's in the expressions:

$i_1 = i_2 = \frac{V}{4R}$

$i_3 = i_4 = \frac{V}{2R}$

and don't forget to include expressions for the currents $i_5$ and $i_6$ .

 

[quantum2013]

That's the idea, although technically you should include the R's in the expressions:

$i_1 = i_2 = \frac{V}{4R}$

$i_3 = i_4 = \frac{V}{2R}$

and don't forget to include expressions for the currents $i_5$ and $i_6$ .

$i_5= \frac{V}{2R}$
$i_6=0$ because $i_6=-i_6$

Why are you including R's in the expressions if the question asks for magnitude of the currents in V?

 

[quantum2013]

gneill how would you go about answering parts 4 and 5 of the question?

 

[gneill]

$i_5= \frac{V}{2R}$
$i_6=0$ because $i_6=-i_6$

Why are you including R's in the expressions if the question asks for magnitude of the currents in V?

Because R is some resistor constant (a value that is specified only as a symbol in the problem statement). V is in volts, and Volts over Resistance yields current.

 

[gneill]

gneill how would you go about answering parts 4 and 5 of the question?

Why don't you make an attempt? We can't do your homework for you here...