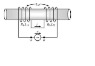
SUMMARY
The discussion focuses on calculating the mutual inductance between two inductors with a magnetic coupling factor of k = 0.75. The participants emphasize the importance of dot notation for determining the orientation of the inductors' windings, which affects the sign of the mutual inductance. The formulas for total inductance, L = L1 + L2 ± 2M, are introduced, highlighting the distinction between concordant and discordant coupling. Ultimately, the conclusion is that without specific values for self-inductances L1 and L2, only a symbolic result can be provided.
PREREQUISITES
- Understanding of mutual inductance and its significance in electrical circuits.
- Familiarity with dot notation for coupled inductors.
- Knowledge of inductance formulas, specifically L = L1 + L2 ± 2M.
- Basic principles of AC circuits, including sinusoidal current.
NEXT STEPS
- Research "mutual inductance dot notation" for comprehensive tutorials and visual aids.
- Study the derivation and application of the formulas for total inductance in coupled circuits.
- Explore the impact of different winding configurations on mutual inductance.
- Investigate methods for measuring self-inductance in practical circuits.
USEFUL FOR
Electrical engineering students, circuit designers, and anyone involved in analyzing or designing inductive components in AC circuits.