Mutual Inductance Homework Solution

[danilorj]

Homework Statement

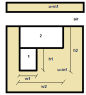
Derive an expression for the mutual inductance ,L12, for the case of the figure, assuming a current distribution:
J_{2}(x)= F_{2}(x), h1<x<h2
or
I_{2}(x)= ∫^{h_2}_{h_1} F_{2}(x)w_{2}dx

Homework Equations

L_{12}(x)=∅_{12}(x)/ i_{2}(x)

The Attempt at a Solution

In fact I don't know why the problem gives this current distribution. For me the final expression of the mutual inductance does not depend on current. And I don't know either the behavior of the flux lines. The final expression for the mutual I found is L_{12}=μ_{0}*(h_{2}-h_{1})w_{1} / (g+h_{2})

 

[rude man]

No idea what this picture represents. Coils? You're right, the mutual inductance between two wired arrangements is not a function of current unless paramagnetics are involved.

 

[danilorj]

The problem is not clear at all on specifying what really this picture means. But I guess the region that is in bege is the magnetic core whose permeability is infinity. And 1 and 2 are cross section of rectangular conductors embedded in the core. Then, for somehow, it makes a currrent density to go through a conductor 2 and it will generate a magnetic flux across conductor 1, for this magnetic flux that is mutual inductance associated. That is what a problem is asking for.