N lines separate the plane into...

[r0bHadz]

Homework Statement

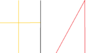
Show that n lines separate the plane into (n^2+n+2)/2 regions if no two of these lines are parallel and no three pass through a common point

Homework Equations

The Attempt at a Solution

Look at my picture. The one on the left separates into 4 reigions, the one on the right separates into 3. Yet using the same n=2 lines. I don't understand

 

[Orodruin]

Your drawing is finite. The plane is not.

Extend the lines to infinity.

 

[r0bHadz]

Your drawing is finite. The plane is not.

Extend the lines to infinity.

gahh I am an idiot. thank you lol

 

[Orodruin]

gahh I am an idiot. thank you lol

Don’t worry. I have seen hundreds of posts like this so you are not alone. Sometimes you need to be pointed to the trees in the forest.

 

[mathwonk]

moreover it seems that exactly 2n of the regions are unbounded, and (1/2)(n-1)(n-2) are bounded. The number of bounded regions, or "holes" in the figure, interestingly gives the genus formula for a complex projective plane curve of degree n. This is the argument by degenerating a curve of degree n into n general lines. At first I was puzzled as to why the number of regions was larger than the genus, since, knowing the genus formula, I thought I it would be also the answer to your problem.