Need help deriving an expression for dy/dt

[Blake_ap1]

Homework Statement

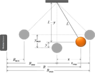
I need help finding the appropriate expression to use to add a "new calculated column" to produce a vertical velocity vs time graph in Logger Pro. The lab consisted of a ball tied to a rope, creating a pendulum. The Go! Motion sensor was set up to record the oscillations. The sensor recorded horizontal displacement and horizontal velocity. The x position vs time was calculated using the expression x = "R" - Ravg. The horizontal velocity was calculated using the expression y = L - sqrt(L^2-"x"^2).

I do not know what expression to use to find the vertical velocity.

R avg = (Rmax + Rmin) / 2 = 1.476 m. The section reads.

The horizontal velocity (vx) of the oscillating object was automatically calculated by the program. To find the vertical velocity (yy), create a new calculated column using the equation derivative("y"). The derivative (or dy/dt) is the rate of change of the vertical position with time. You should be able now to calculate the magnitude (v) of the resultant velocity. What is the appropriate equation for this calculation? Display vx, vy and v together on the same graph and include it in your lab report. Comment on the relationship between the three graphs.

Can someone point me in the right direction? Attatched are releative photos and the lab manual. I am doing Lab 4, and Working on the vertical velocity vs time section on page 25
Relevant equations The attempt at a solution
I'm having trouble Deriving the expression for dy/dt. I've hit a deadlock. I know I have to change things to the manner of y and θ. I know y = L - Lcosθ & x = Lsinθ

I know my expression needs to be along the lines of vy = (LxVx)/ (sqrt(x²+(L-y)²) + Ly)

 

[BvU]

The horizontal velocity was calculated using the expression y = L - sqrt(L^2-"x"^2).

Looks more like a formula for y. It has the name and the dimension of the y in the first drawing.

 

[BvU]

using the equation derivative("y")

Is that an expression your Logger Pro recognizes ? What IS the expression used for the horizontal velocity ?

Can you differentiate $x^2 + (L-y)^2 = L^2$ with respect to time ? ( I mean the analytical formula, not the LogPro expression)

 

[Blake_ap1]

Is that an expression your Logger Pro recognizes ? What IS the expression used for the horizontal velocity ?

Can you differentiate $x^2 + (L-y)^2 = L^2$ with respect to time ? ( I mean the analytical formula, not the LogPro expression)

Sorry, Y position was established using L-sqrt(L^2 - x^2)
Horizontal velocity and position were established with a motion sensor.

I derive the y position formula to obtain the velocity with respect to x. I’m not sure how to derive y with respect to time for dy/dt.
With respect to x I get vy = x/(sqrt(L^2 – x^2))

 

[haruspex]

With respect to x I get vy =

Differentiating one displacement wrt another will not give a velocity. That is dimensionally wrong. It might give you a gradient (and will in this case).

I’m not sure how to derive y with respect to time for dy/dt.

Make an attempt. Use the chain rule.