PhysicsPadawan
- 2
- 0
Homework Statement
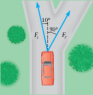
Two forces are applied to a car in an effort to move it, as shown in the figure below. (Let
F1 = 430 N (10 degrees)
and
F2 = 356 N. (30 degrees)
Assume up and to the right are in the positive directions.)
(a) What is the resultant vector of these two forces?
magnitude=?
° to the right of the forward direction=?
(b)If the car has a mass of 3,000 kg, what acceleration does it have? Ignore friction.
Homework Equations
(430sin(10)) + 356sin(30)=252.67x
(430cos(10)) + 356cos(30)=731.78y
a=(731.78)/(3000)
F=ma
angle = tan-1((731.78y)/(252.67x)) ??[/B]
The Attempt at a Solution
For part a I got 774.17N for the magnitude and it was correct
For part b I got 0.244 for the acceleration and it was correct
But I can not for the life of me solve for angle to the right of the forward direction
[/B]