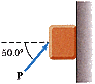Need help on a max and min force question

[pcandrepair]

A block of mass 2.00 kg is pushed up against a wall by a force P that makes a 50.0° angle with the horizontal as shown below. The coefficient of static friction between the block and the wall is 0.258. (The attached picture might help).

A.) Determine the possible values for the magnitude of P that allow the block to remain stationary.
P max =
P min =

Any help would be greatly appreciated. Thanks!

 

[Doc Al]

What forces (vertical and horizontal) act on the block?

 

[pcandrepair]

The force in the y-direction(vertical) would be Py = P(sin(50)) and in the x-direction(horizontal), the force would be Px = P(cos(50)). The x-direction would also include the normal force, n, and the y-direction would include gravity*mass, mg.

 

[pcandrepair]

I forgot to add that the x-direction would also include the normal force, n, which would be located along the negative x-axis. The y-direction would include gravity*mass, mg, on the negative y-axis.

 

[Doc Al]

What about friction? What's its magnitude and which way does it act?

 

[pcandrepair]

Friction is the normal*coefficient of friction. I found that the normal force is n = Pcos50. To find the max wouldn't you make friction negative because it would be acting downwards and vice versa for minimum? I just not sure how to put all these into an equation to solve for P. I also know that the acceleration would be zero.

 

[Doc Al]

Friction is the normal*coefficient of friction. I found that the normal force is n = Pcos50. To find the max wouldn't you make friction negative because it would be acting downwards and vice versa for minimum?

Exactly right.

I just not sure how to put all these into an equation to solve for P. I also know that the acceleration would be zero.

Just set vertical forces equal to zero and you can solve for P.

 

[pcandrepair]

I don't think I'm getting the right answers...So would the equation (for the max) be
( Psin50 - (-friction(Pcos50)) - mg = 0 )? And the Psin50 and mg would cancel out because they would equal zero? I don't think I'm doing this right...

 

[Doc Al]

So would the equation (for the max) be
( Psin50 - (-friction(Pcos50)) - mg = 0 )?

So far, so good--except for that double minus sign. I'd write it like this:
$$P\sin{50} - \mu P\cos{50} - mg = 0$$

Now just solve for P.

And the Psin50 and mg would cancel out because they would equal zero?

Why would they cancel?

 

[pcandrepair]

I thought that's what you meant by set the vertical forces to zero because Psin50 and mg are vertical forces. When i solve for Pmax I'm getting 154.282 N. If you made the friction positive to find the min wouldn't that make the force the same but just negative?

 

[Doc Al]

I thought that's what you meant by set the vertical forces to zero because Psin50 and mg are vertical forces.

But friction is a vertical force also! There are three vertical forces, which add to zero.

When i solve for Pmax I'm getting 154.282 N.

I don't see how you got this result.

If you made the friction positive to find the min wouldn't that make the force the same but just negative?

No.

 

[pcandrepair]

If the vertical forces, Psin50, -friction, and -mg add to zero, i don't see how you can solve for P or how it could be a reasonable answer. I think I'm making this harder than it is :S

 

[Doc Al]

Solve the equation I gave in post #9. The only unknown is P; everything else is just numbers.

 

[pcandrepair]

Psin50 + P(.258)(cos50) - 2kg(9.8) = 0

Psin50 + P(.258)(cos50) = 19.6

2P = 19.6 / (cos50)(sin50)(.258)

P = 154.282 / 2
(I forgot to divide by two last time i got 154.282)

P = 77.141 N

Or am i making some stupid basic math mistake?

 

[Doc Al]

Psin50 + P(.258)(cos50) - 2kg(9.8) = 0

That first + sign should be a minus sign.

Psin50 + P(.258)(cos50) = 19.6

That should be:
Psin50 - P(.258)(cos50) = 19.6

2P = 19.6 / (cos50)(sin50)(.258)

No good. Factor out the P.

For example, note that Xa - Xb = X(a - b)

 

[pcandrepair]

I always seem to make those basic math mistakes! I entered my answers and they were correct. Thank you for all your help Doc Al!

 

[Doc Al]

Excellent. Why don't you mark this one solved.

 

[pcandrepair]

Actually, the is a part b and it has the same numbers except for an angle of 13 degrees from the horizontal. This time I'm getting a negative number for some reason

 

[Doc Al]

If the only difference is that the new angle is 13 degrees (instead of 50), then you can solve it in exactly the same way.

 

[pcandrepair]

When i do that i get P = 19.6 / -.02 which turned out to be -714 ish

 

[Doc Al]

When i do that i get P = 19.6 / -.02 which turned out to be -714 ish

You're right. This one's trickier.

First off, solve for the minimum force P. That should be no problem.

In solving for the maximum, we assumed that we could take the static friction to it's maximum value. That was true at 50 degrees, but is not true for this angle.

 

[pcandrepair]

For the minimum force P i got 41.1472 N.

 

[pcandrepair]

But this angle is still in the 3rd quadrant which you would think still work, so i can't think of how to solve this.

 

[pcandrepair]

Would the max equal zero for this angle because it is not possible for the object to slide up no matter what force is applied?

 

[Doc Al]

You are correct that it won't slide up it you keep pressing it harder--but that means there is no maximum value for the force. Press as hard as you want!

Since the maximum friction is always greater than the vertical component of P (since $\mu \cos{13} > \sin{13}$), you'll always have enough friction to prevent motion (as long as P is above the minimum). For any given value of P, the friction only has to equal $P\sin{13} - mg$, which is less than the maximum.