Need help on integration question i found on net

[Keval]

Question is in orange, answer is in black.

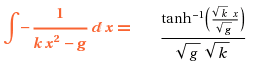
I got no idea how they got this answer :\

The way I am trying is using a substition of kx^2 = gsin\theta

Just the one question i can't get my head aroung in this exercise step by step method would be appreciated

 

[tiny-tim]

Hi Keval!

Not sin, but tanh … try substituting x√(k/g) = tanhu

 

[g_edgar]

With denominator instead k x^2 + g you get an arctan answer, right? Use the same steps on this one and get an atanh answer.

 

[Keval]

someone check this out for me ??

-\frac{1}{k} \int \frac{dx}{x^2-\frac{g}{k}}


to simplify i let\frac{g}{k}=m^2 to get


-\frac{1}{k}\int \frac{dx}{x^2-m^2}=-\frac{1}{k}\int \frac{dx}{(x-m)(x+m)}


Using partial fractions i got
\int \frac{dx}{x^2-m^2}=\int \frac{\frac{1}{2m}}{x-m}dx+\frac{-\frac{1}{2m}}{x+m}dx=



\frac{1}{2m}\ln|x-m|-\frac{1}{2m}\ln|x+m|=\frac{1}{2m}\ln \left| \frac{x-m}{x+m}\right|=

-\frac{1}{m}\cdot \frac{1}{2}\ln \left|\frac{x+m}{x-m} \right|=-\frac{1}{m}\tanh^{-1}\left( \frac{x}{m}\right)

\frac{1}{km}\tanh^{-1}\left( \frac{x}{m}\right)=\frac{1}{\sqrt{gk}}\tanh^{-1}\left(\sqrt{\frac{k}{g}}x \right)

 

[tiny-tim]

Hi Keval!

Yes, your partial fractions method is fine.

But it would be far quicker to start "let x√(k/g) = tanhu, dx√(k/g) = sech²u du" …

try it! ​