Physrook 09
- 4
- 0
Question Details:
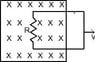
A circuit is pulled with a 16-N force toward the right to maintain a constant speed v. At the instant shown, the loop is partially in and partially out of a uniform magnetic field that is directed into the paper. As the circuit moves, a 6.0-A current flows through a 4.0- ohm resistor. What is the direction of the current flow? What is the magnitude of v? Diagram attached.
A circuit is pulled with a 16-N force toward the right to maintain a constant speed v. At the instant shown, the loop is partially in and partially out of a uniform magnetic field that is directed into the paper. As the circuit moves, a 6.0-A current flows through a 4.0- ohm resistor. What is the direction of the current flow? What is the magnitude of v? Diagram attached.