Need some help on Circuit modeling(1 sample)

[genxium]

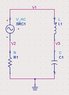
I'm learning circuit modeling recently, and got stuck by a simply serial circuit sample(shown in the attachment), here're equations I wrote for the sample, but I have no idea what initial conditions and algorithm I can use to solve it, could anyone give me a hand or some tips?

i_{21}+{\int_0}^t \frac{V_3-V_1}{L} d\tau =0
i_{12}+\frac{GND-V_2}{R} =0
{\int_0}^t \frac{V_1-V_3}{L} d\tau + C \cdot (\frac{dGND}{dt}-\frac{dV_3}{dt}) =0
C \cdot (\frac{dV_3}{dt}) + \frac{V_2-GND}{R}=0

where GND=0 V is constant, I see that i_{12}=-i_{21} can be used to reduce the equations, but then the remaining equations are 2nd order diff equations, how do computers solve this?

{\int_0}^t \frac{V_2-V_1}{L} d \tau = \frac{-V_2}{R}
{\int_0}^t \frac{V_1-V_3}{L} d\tau + C \cdot -\frac{dV_3}{dt} =0
C \cdot (\frac{dV_3}{dt}) + \frac{V_2}{R}=0

 

[genxium]

I just read some tutorial of numerical solutions, but the easily found materials are all about ordinary diff equations of only 1 unknown function, could anyone tell me some tutorial that shows the idea to multiple unknown functions' diff equation(numerical solution)?

 

[jim hardy]

i guess you're stuck at integrating those diads like (V2 - V1) and (V1 - V3) ?

see if you don't just integrate them separately and add..

http://en.wikipedia.org/wiki/Sum_rule_in_integration

 

[genxium]

i guess you're stuck at integrating those diads like (V2 - V1) and (V1 - V3) ?]

Uhm... I don't think this is the main issue here, take derivatives of these diff equations, then

\frac{V_2-V_1}{L}=-\frac{dV_2}{R \cdot dt}

\frac{V_1-V_3}{L}+C \cdot -\frac{d^2V_3}{dt^2}=0

C \cdot \frac{dV_3}{dt}+\frac{V_2}{R}=0

and want to get numerical solutions for V_1(t),V_2(t),V_3(t).