bengt2665
- 4
- 0
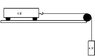
The weight of the cart is 4 N. The weight of the hanging mass is 4 N.
Friction of the cart on the track is a constant force of 2 N magnitude.
The mass of the string, the mass of the pulley, and the friction of the pulley can be neglected.
What is the magnitude of the acceleration of the cart if g is the free-fall acceleration?
Picture attached.
The answer is to be given in terms of g.
Okay, here's what I have so far:
By drawing a free body diagram I manage to get these two equations for the forces acting on both the cart and the hanging mass:
I'm assuming positive acceleration to the right of the cart and down for the mass.
For the cart: T - Ff = ma
For the mass: T - mg = ma
(since they have the same weight, there is only one m)
We know that the weight of these two is 4N each so for both, 4 = ma (i'm predicting this might not be right...)
I'm having trouble applying their given information (4N weight for both masses) with the equations I'm coming up with, for example I don't know what this 4N corresponds to...
Is it 4N = m.a for the cart and 4N = mg for the hanging mass?
How do I apply the information they are giving me?
Thanks!
Friction of the cart on the track is a constant force of 2 N magnitude.
The mass of the string, the mass of the pulley, and the friction of the pulley can be neglected.
What is the magnitude of the acceleration of the cart if g is the free-fall acceleration?
Picture attached.
The answer is to be given in terms of g.
Okay, here's what I have so far:
By drawing a free body diagram I manage to get these two equations for the forces acting on both the cart and the hanging mass:
I'm assuming positive acceleration to the right of the cart and down for the mass.
For the cart: T - Ff = ma
For the mass: T - mg = ma
(since they have the same weight, there is only one m)
We know that the weight of these two is 4N each so for both, 4 = ma (i'm predicting this might not be right...)
I'm having trouble applying their given information (4N weight for both masses) with the equations I'm coming up with, for example I don't know what this 4N corresponds to...
Is it 4N = m.a for the cart and 4N = mg for the hanging mass?
How do I apply the information they are giving me?
Thanks!