BitterX
- 35
- 0
Mu1 is the friction coefficient , I'm sure I did it wrong because I got the acceleration isn't dependent on it, and it doesn't make sense.
disregard the axis in the drawing - it's for another question.
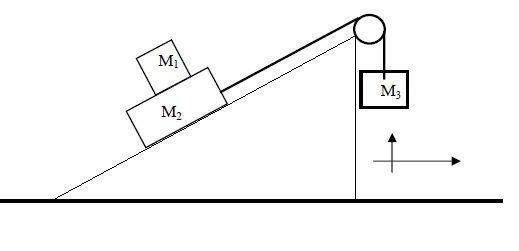
Find an expression for the acceleration of the system when there is no relative movement between M1 and M2
(same acceleration and velocity?)
ΣF =ma
View attachment 1.doc
disregard the axis in the drawing - it's for another question.
Homework Statement
Find an expression for the acceleration of the system when there is no relative movement between M1 and M2
(same acceleration and velocity?)
Homework Equations
ΣF =ma
The Attempt at a Solution
View attachment 1.doc