dharavsolanki
- 77
- 0
Homework Statement
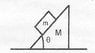
A block of mass m lies on a wedge of mass M as shown in figure. Answer the following parts separately.
(a) - With what minimum acceleration must the wedge be moved towards right horizontally so that the block m falls freely?
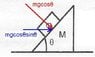
(b) - Find the minimum friction co-efficient required between M and ground so that it does not move while block m slips down on it.
Variables - Mu(ground), a_m and a_M
Homework Equations
F = ma
The Attempt at a Solution
Not able to start anything anywhere.
For (a)
- - - - -
I can't make equations out of the situation, but I am getting a weird feeling it is the same thing as a satellite. It keeps on falling towards the earth, only that the Earth keeps on receding. The only difference being that the falling object not reaching the ground was "Earth's curvature" in one case and "Slope of wedge" in the other. Not sure how to translate this idea into equations.
For (b)
- - - - -
I have attempted it, but it gets too complicated, the normal reaction between the two wedges changes the normal reaction between the surfaces and such. How should I carry on with this?