jisbon
- 475
- 30
- Homework Statement
- -
- Relevant Equations
- -
Was just practicing some problems on the Fundamentals of Electric Circuits, and came across this question.
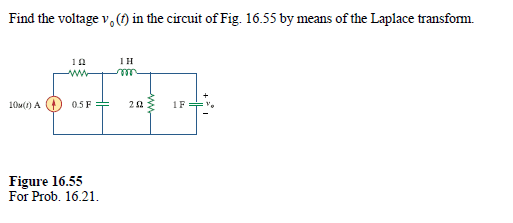
I understand I will have to transform to the s domain circuit, which looks something like this:
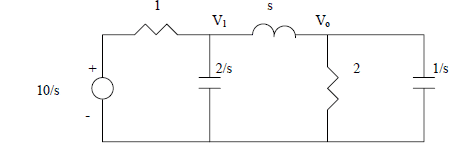
Then doing nodal analysis, I will get the following for the first segement
(10/s-V1)/1 = (V0-V1)/s + V1/(2/s)
However, the answer booklet states that it should be: (10/s-V1)/1 = (V0-V1)/s + V0/(2/s)
I'm unsure if the answer booklet is wrong though,because I thought I was pretty confident in nodals until I see the answer.
What are the problems with my concepts in this case? Thanks
I understand I will have to transform to the s domain circuit, which looks something like this:
Then doing nodal analysis, I will get the following for the first segement
(10/s-V1)/1 = (V0-V1)/s + V1/(2/s)
However, the answer booklet states that it should be: (10/s-V1)/1 = (V0-V1)/s + V0/(2/s)
I'm unsure if the answer booklet is wrong though,because I thought I was pretty confident in nodals until I see the answer.
What are the problems with my concepts in this case? Thanks
Last edited by a moderator: