You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Challenging Integrals: Seeking Hints and Solutions
- Thread starter athrun200
- Start date
-
- Tags
- Elementary Integral
Physics news on Phys.org
romsofia
Gold Member
- 599
- 330
athrun200 said:Homework Statement

Homework Equations
The Attempt at a Solution
Well, I just want some hint.
It seems substitution doesn't work.(I can't think of any suitable substitution)
These all seem to be like special functions, like for the first one, http://press.princeton.edu/books/maor/chapter_10.pdf however, you probably know that :x!
Last edited by a moderator:
SammyS
Staff Emeritus
Science Advisor
Homework Helper
- 11,987
- 1,579
Try changing the order of integration. Is that one of the subjects that is covered in the section of the textbook in which you found these problems?
athrun200
- 275
- 0
SammyS said:Try changing the order of integration. Is that one of the subjects that is covered in the section of the textbook in which you found these problems?
This chapter is about Multiple integrals, but it doesn't cover these special functions(Maybe the textbook assume we know these already).
It seems after changing the order, nothing change.
Take the first one as an example.
Attachments
SammyS
Staff Emeritus
Science Advisor
Homework Helper
- 11,987
- 1,579
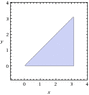
Looking at problem 29. as it is given: \displaystyle \int_{y=0}^{\pi} \int_{x=y}^{\pi}\,\frac{\sin\,x}{x}\,dx\,dy\,, what is the region over which the integration is to be done?
For any given y, x goes from the line x = y (the same as y = x) to the vertical line y = π. y goes from 0 (the x-axis) to π.
Therefore, this is the region in the xy-plane bounded by the x-axis, the line x = π and the line y = x.
That's not the same region you integrated over after you changed the order of integration. You integrated over the region bounded by the y-axis, the line y = π and the line y = x.
For the correct region, switching the order of integration will eliminate having to integrate "special functions".
For any given y, x goes from the line x = y (the same as y = x) to the vertical line y = π. y goes from 0 (the x-axis) to π.
Therefore, this is the region in the xy-plane bounded by the x-axis, the line x = π and the line y = x.
That's not the same region you integrated over after you changed the order of integration. You integrated over the region bounded by the y-axis, the line y = π and the line y = x.
For the correct region, switching the order of integration will eliminate having to integrate "special functions".
- 15,524
- 769
Do this right, athrun200, and this same technique will apply to all four of those problems.SammyS said:For the correct region, switching the order of integration will eliminate having to integrate "special functions".
SammyS
Staff Emeritus
Science Advisor
Homework Helper
- 11,987
- 1,579
romsofia
Gold Member
- 599
- 330
SammyS said:Looking at problem 29. as it is given: \displaystyle \int_{y=0}^{\pi} \int_{x=y}^{\pi}\,\frac{\sin\,x}{x}\,dx\,dy\,, what is the region over which the integration is to be done?
For any given y, x goes from the line x = y (the same as y = x) to the vertical line y = π. y goes from 0 (the x-axis) to π.
Therefore, this is the region in the xy-plane bounded by the x-axis, the line x = π and the line y = x.
That's not the same region you integrated over after you changed the order of integration. You integrated over the region bounded by the y-axis, the line y = π and the line y = x.
For the correct region, switching the order of integration will eliminate having to integrate "special functions".
While I'm not the OP, I have to say thanks as that is a cool technique that I did not know of! Thanks!
athrun200
- 275
- 0
Sorry for late reply. Recently, I am learning a new topic call moment of inertia and encounter some trouble. If you are also good at this, please help me. https://www.physicsforums.com/showthread.php?p=3405893#post3405893"
Now let see if I can do it correctly.
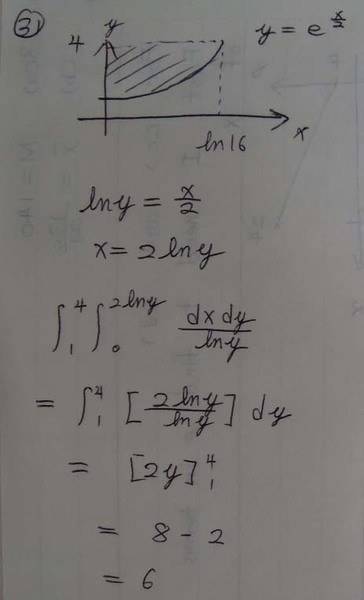
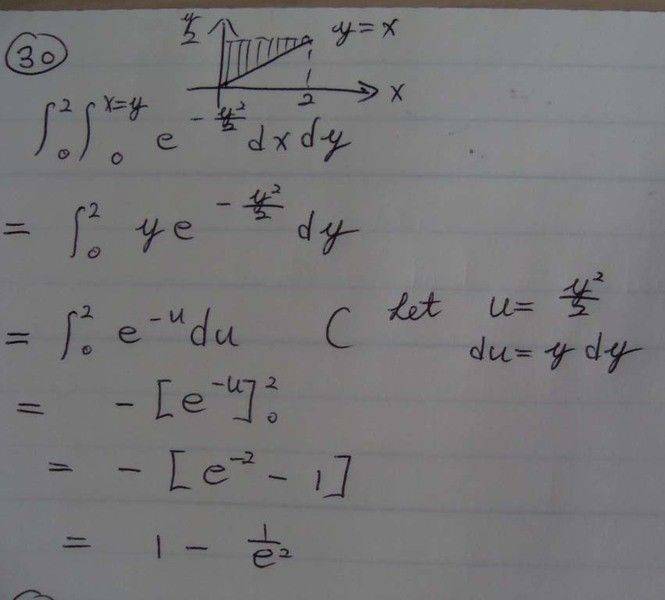
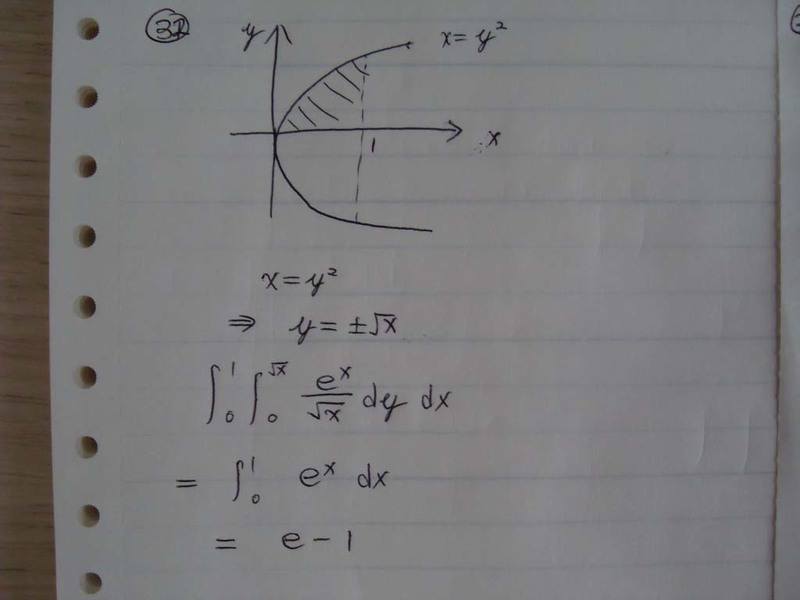
Now let see if I can do it correctly.
Attachments
Last edited by a moderator:
- 15,524
- 769
Excellent. You got all three.
athrun200
- 275
- 0
D H said:Excellent. You got all three.
I am so happy that I understand this section now
SammyS
Staff Emeritus
Science Advisor
Homework Helper
- 11,987
- 1,579
athrun200 & romsofia,
Glad that you now understand this.D H,
Thanks for checking in on these problems! I'm traveling & have been away from computer access for a few days.
Glad that you now understand this.D H,
Thanks for checking in on these problems! I'm traveling & have been away from computer access for a few days.
athrun200
- 275
- 0
SammyS said:athrun200 & romsofia,
Glad that you now understand this.
D H,
Thanks for checking in on these problems! I'm traveling & have been away from computer access for a few days.
I start another topic on integral and encounter some problems.
And these questions are still haven't been answered yet.
https://www.physicsforums.com/showthread.php?t=514747"
https://www.physicsforums.com/showthread.php?t=514734"
Last edited by a moderator:
Similar threads
- Replies
- 6
- Views
- 2K
- Replies
- 4
- Views
- 3K
- Replies
- 4
- Views
- 1K
- Replies
- 15
- Views
- 2K
- Replies
- 4
- Views
- 2K
- Replies
- 23
- Views
- 2K
- Replies
- 1
- Views
- 1K
- Replies
- 7
- Views
- 2K
- Replies
- 8
- Views
- 2K
Hot Threads
-
Prove that the integral is equal to ##\pi^2/8##
- Started by Meden Agan
- Replies: 105
- Calculus and Beyond Homework Help
-
Solve this problem that involves induction
- Started by chwala
- Replies: 7
- Calculus and Beyond Homework Help
-
Finding the modulus and argument of ##\dfrac{a}{(b±ci)^n}##
- Started by chwala
- Replies: 17
- Calculus and Beyond Homework Help
Recent Insights
-
Insights Why Entangled Photon-Polarization Qubits Violate Bell’s Inequality
- Started by Greg Bernhardt
- Replies: 26
- Quantum Interpretations and Foundations
-
Insights Quantum Entanglement is a Kinematic Fact, not a Dynamical Effect
- Started by Greg Bernhardt
- Replies: 11
- Quantum Physics
-
Insights What Exactly is Dirac’s Delta Function? - Insight
- Started by Greg Bernhardt
- Replies: 3
- General Math
-
Insights Relativator (Circular Slide-Rule): Simulated with Desmos - Insight
- Started by Greg Bernhardt
- Replies: 1
- Special and General Relativity
-
Insights Fixing Things Which Can Go Wrong With Complex Numbers
- Started by PAllen
- Replies: 7
- General Math
-
Insights Fermat's Last Theorem
- Started by fresh_42
- Replies: 105
- General Math