gcombina
- 157
- 3
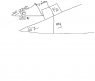
A 250-N force is directed horizontally as shown to push a 29-kg box up an inclined plane at a constant speed. Determine the magnitude of the normal force, FN, and the coefficient of kinetic friction, µk.
So, I know I have to find the vertical and parallel forces
Vertical: Fn and 250 sin of angle (where is the angle symbol?)
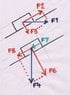
so, if you look at the second picture, that is where I get stucked. Is "mg" also part of the parallel force?
So, I know I have to find the vertical and parallel forces
Vertical: Fn and 250 sin of angle (where is the angle symbol?)
so, if you look at the second picture, that is where I get stucked. Is "mg" also part of the parallel force?
Attachments
Last edited: