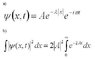Normalization
- 23
- 0
All the relevant information about the problem is in the attachment.
I just have a problem with the first step, my question it:
How is b true? I would have thought that the second part of the exponential function would be taken outside of the integral as well as A since you're taking the integral with respect to x and why is it TWO TIMES abs(A)^2 and why does the absolute value disappear from the exponent of the integrand?
PS: This is my first time on the forum so I appologize in advance if I haven't been clear enough etc. Also I'm trying to teach myself so I don't have a professor to turn to etc.
I just have a problem with the first step, my question it:
How is b true? I would have thought that the second part of the exponential function would be taken outside of the integral as well as A since you're taking the integral with respect to x and why is it TWO TIMES abs(A)^2 and why does the absolute value disappear from the exponent of the integrand?
PS: This is my first time on the forum so I appologize in advance if I haven't been clear enough etc. Also I'm trying to teach myself so I don't have a professor to turn to etc.