hobo skinoski
- 2
- 0
Four resistors are connected to a battery as shown in the figure. The current in the battery is I, the battery emf is E, and the resistor values are R1 = R, R2 = 2R, R3 = 4R, and R4 = 3R.
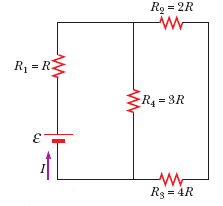
-Determine the potential difference across each resistor in terms of E.
-Determine the current in each resistor in terms of I.
-In the limit that R3 → infinity, what are the new values of the current in each resistor in terms of I, the original current in the battery?
V=IR
Rtotal=R1+R2+... (Series)
1/2Rtotal=1/R1 + 1/R2 ... (Parallel)
I've tried a bunch of different combos, and I'm just wondering if there is some sort of way to do this.
-Determine the potential difference across each resistor in terms of E.
-Determine the current in each resistor in terms of I.
-In the limit that R3 → infinity, what are the new values of the current in each resistor in terms of I, the original current in the battery?
Homework Equations
V=IR
Rtotal=R1+R2+... (Series)
1/2Rtotal=1/R1 + 1/R2 ... (Parallel)
The Attempt at a Solution
I've tried a bunch of different combos, and I'm just wondering if there is some sort of way to do this.