I Nozzle Reaction Forces: Explaining the Resultant Force

[Timtam]

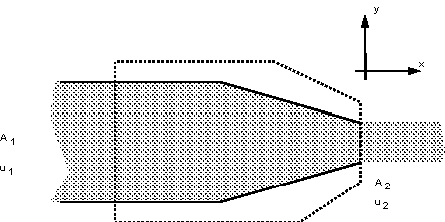
I have been reading many examples of control volume calculations regarding nozzles

They all end up with a reaction force on the nozzle in the direction of the flow.

I can't understand this from a Conservation of momentum perspective.
I would expect that the reaction force, by Newtons third law, would be opposite the mass that was accelerated in. This is how many people explain it but it doesn't equate with the control volume result.
Can anyone review my attempt at a solution and critique

Attempt at a solution
It appears the resultant force has nothing to do with the flow acceleration or pressure drop
Much like the flow around a bend, it is due to the change in flow direction.
More specifically, it is the x direction components of the resultant force due to the angle of the nozzle changing the flows direction.

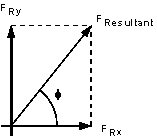
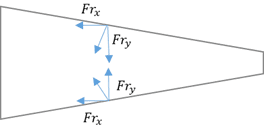
(Y direction components being equal and opposite directions cancel out.)

Why doesn't the flow "acceleration" require a resultant force?
Even though the velocity of the fluid has increased at the nozzle, the flow has experienced no 'real' acceleration so no resultant force is required.
While the velocity at P2 has increased, the volumetric flow rate Q has not. It has only changed in area and by continuity- velocity has increased.

The x-direction flow rate Q into and out of the control volume is the same - so there is no acceleration.

The pressure gradient force?

The flow rate Q is fully accounted for by the pressure difference P1-P2 over the original area

Why do firefighters brace a hose forward ?

I don't think they do I think they actually brace it down.

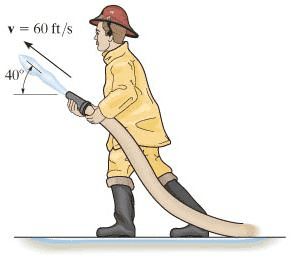
This is because a hose initially runs along the ground then up the firefighter.
So again there is resultant forces from changing a fluids direction initially up (the resultant force is provided by gravity and against the ground) once it is traveling up to make it horizontal again the firefighter must provide a downward force above the hose to change its direction downward again.

 

[BvU]

The flow rate Q is fully accounted for by the pressure difference P1-P2 over the original area

How so ?
Check this one

Nobody would try to use a nozzle that isn't solidly connected to the hose, right ?

The firefighter has nothing to do with it. Unless he has to use a hose where the nozzle isn't fixed -- and that's hopeless.

 

[sophiecentaur]

If the nozzle is of smaller diameter than the hose (usual setup?) then the water will be accelerating as it goes through the taper and emerge at a higher speed than it had in the hose, which involves a forward force acting on the water as it flows through. That will require a constant reaction force on the hose to stop it moving backwards. This is the same principle as a rocket or jet engine.
It is not necessary to consider the details of the passage of the water and the details of the pipe / nozzle to get a good, near enough answer. All that's necessary is to know the entry and exit diameters and the flow rate (and density of course).
Edit: the direction of the nozzle will affect what actual force is acting on the nozzle. If it is pointed at right angles to the hose then forces on the hose will cancel and all the reaction force will be on the nozzle. If the hose and nozzle are totally aligned, the reaction force will be upstream, on the compressor only. So you could say that the fireman is needed in order to control any lateral force.
That link above explains it well.

 

[Timtam]

Hi @BvU yes that link gives the same answer- it is to the right. You will have the same volumetric flow rate no matter what the size of your nozzle is or whether you have any shape in the control volume at all - in the x -direction the only thing that can change the control volume flow rate Q is the original diameter in and P1-P2

If the nozzle is of smaller diameter than the hose (usual setup?) then the water will be accelerating as it goes through the taper and emerge at a higher speed than it had in the hose, which involves a forward force acting on the water as it flows through. That will require a constant reaction force on the hose to stop it moving backwards

@sophiecentaur yes that is what I thought as well but the reaction force is to the right -forwards not backwards.

 

[sophiecentaur]

Hi @BvU yes that link gives the same answer- it is to the right. You will have the same volumetric flow rate no matter what the size of your nozzle is or whether you have any shape in the control volume at all - in the x -direction the only thing that can change the control volume flow rate Q is the original diameter in and P1-P2
@sophiecentaur yes that is what I thought as well but the reaction force is to the right -forwards not backwards.

The answer is 'to the right' and that is 'backwards' i.e. in the opposite direction to the direction of the water jet. Let's face it, whatever the details, Newton's Third Law has to apply. What I was meaning is that there will be a backwards 'reaction force' because the water is moving forwards BUT the fireman has to resist this force with a forwards Reaction force of his own, to stope the nozzle going backwards due the the 'first' reaction force.

 

[Timtam]

The answer is 'to the right' and that is 'backwards' i.e. in the opposite direction to the direction of the water jet.

I am so confused by this- to the right is in the direction of the flow. I had a look at @BvU example and that says the same what am I missing that this somehow becomes to the left?

 

[sophiecentaur]

I look at the picture of the fireman and he is facing left??

 

[Timtam]

@sophiecentaur the nozzle examples in my attempt at solution are all facing right- The fireman picture in the next section is to explain what I think the fireman is actually bracing against

Have a look at the link @BvU provided if you want to be as confused as I am

How so ?
Check this one

 

[BvU]

The x-direction flow rate Q into and out of the control volume is the same - so there is no acceleration.

How can you say that ? $\dot m$ is the same and $v$ increases considerably. That's what we call acceleration.

 

[Chestermiller]

The upstream pressure is higher than the downstream pressure (Bernoulli). If fluid pressure is acting on the wall of the nozzle (this is the only force acting on the wall), it acts perpendicular to the wall. This means that there is a resultant pressure force on the nozzle wall in the same direction that the fluid is flowing.

 

[Jonathan Scott]

Just imagine what would happen if you cut the pipe just behind the nozzle. I think it's obvious that the nozzle would be propelled strongly in the direction of the water by the forward water pressure inside the walls of the restricted part. However, if you take the whole system of supply, pipe and firmly-attached nozzle you would expect it to be propelled the other way. I don't see any contradiction in that.

 

[Chestermiller]

Just imagine what would happen if you cut the pipe just behind the nozzle. I think it's obvious that the nozzle would be propelled strongly in the direction of the water by the forward water pressure inside the walls of the restricted part. However, if you take the whole system of supply, pipe and firmly-attached nozzle you would expect it to be propelled the other way. I don't see any contradiction in that.

In the latter case, if the hose were perfectly straight, the nozzle would not be propelled at all.

 

[sophiecentaur]

The upstream pressure is higher than the downstream pressure (Bernoulli). If fluid pressure is acting on the wall of the nozzle (this is the only force acting on the wall), it acts perpendicular to the wall. This means that there is a resultant pressure force on the nozzle wall in the same direction that the fluid is flowing.

That argument sounds convincing until you consider the momentum transfer situation. On the way out of the nozzle, the velocity has increased and the mass flow rate is the same so doesn't that mean momentum has increased on the way through the nozzle? That requires pressure / force and, if the nozzle is pointing off the axis of the hose, there would be a force away from the direction of the jet. The same thing happens with a rocket (doesn't it?) where net reaction force on the inside of the combustion chamber produces a driving force.
The pressure consideration also needs fluid velocity and/or an area in order to work out the Force

 

[A.T.]

The same thing happens with a rocket (doesn't it?) where net reaction force on the inside of the combustion chamber produces a driving force.

The combustion chamber is closed at one end, and the nozzle is expanding in the flow direction, not narrowing like on the hose. That's where the propulsive force acts:

In the case of the hose those pressure forces act on the upstream fluid, not the nozzle. The net pressure force on the hose-nozzle itself is with the flow.

 

[Chestermiller]

That argument sounds convincing until you consider the momentum transfer situation. On the way out of the nozzle, the velocity has increased and the mass flow rate is the same so doesn't that mean momentum has increased on the way through the nozzle?

The only force that the fluid exerts on the nozzle body is pressure. The momentum increase of the fluid affects the fluid pressure upstream within the nozzle, but, treating the nozzle as a free body, it is only the fluid pressure that determines the axial force on the nozzle (aside from the tension at the hose connection). As long as the fluid pressure within the nozzle is higher than the pressure outside the nozzle, the axial force that the fluid exerts on the nozzle will be in the positive flow direction, irrespective of what is happening with the momentum exchanges of the fluid.

Certainly the momentum increase affects the pressure of the fluid within the nozzle. But, as far as the nozzle body knows, it is only the fluid pressure that it feels.

 

[sophiecentaur]

The combustion chamber is closed at one end, and the nozzle is expanding in the flow direction, not narrowing like on the hose. That's where the propulsive force acts:

In the case of the hose those pressure forces act on the upstream fluid, not the nozzle. The net pressure force on the hose-nozzle itself is with the flow.

Yes - there is a difference but isn't that because of the expanding gases in the case of a rocket? There is still acceleration of the water in the nozzle and acceleration requires a force in the direction of that acceleration. That force must have an N3 companion. Where does that act? I suggest backwards, or we have a new method of propulsion.
This video might be of interest if people think the force on the nozzle is forward. The end of the hose does just what the above link predicts.

 

[A.T.]

There is still acceleration of the water in the nozzle and acceleration requires a force in the direction of that acceleration. That force must have an N3 companion. Where does that act?

On the upstream fluid, as already explained.

This video might be of interest if people think the force on the nozzle is forward.

This tells you nothing about the pressure force on the nozzle, because there is also hose tension acting on the nozzle. The relevant experiment would be to separate the nozzle off the hose, as already explained.

 

[sophiecentaur]

The only force that the fluid exerts on the nozzle body is pressure.

Those two quantities are not the same so they can't be equated like that. The force is, of course, due to the water pressure but not just the static pressure. The fact is, there has to be an N3 pair somewhere, to explain the acceleration of the water exiting the nozzle. You have to agree that it is going faster at the tip than through the hose. If you can't address the N3 issue then you have no valid explanation.
You are right in your initial assumption about what happens when the end of the hose is blocked off (the static pressure will cause a force that could push the end off the hose or just burst it).

I have written a number of replies to this but they have all sampled too much. Bottom line is that there is a force acting on the hose in that video (and many more), that makes it snake from side to side. You can do the experiment with a normal garden hose, with a natural curve in it and held a metre or so from the nozzle. The nozzle moves away from the direction of the jet. A force acting only on the inside of the nozzle would simply stretch the hose and make it straight - as in blowing up a sausage balloon. The force which causes this snaking is from side to side and not forward. It has to arise from the Bernoulli effect at the nozzle exit and it is not in the direction of the hose.
You could achieve the same sort of motion as in a Hero Steam Engine, using water instead of steam. The same N3 explanation would apply.

The above link with the curved nozzle calculation is pretty straightforward and accounts for all of this, doesn't it?

 

[Timtam]

How can you say that ? ˙mm˙\dot m is the same and vvv increases considerably. That's what we call acceleration.

Agreed I could have said that better. Ok in your control volume - As others have suggested, take away the nozzle all together (or replace it with a solid wood block)- assuming the entry fixed is and the exit parameters are fixed so keeping the pressure difference-The "acceleration" the parcel experiences is only due to P1 and P2.

The only force that the fluid exerts on the nozzle body is pressure. The momentum increase of the fluid affects the fluid pressure upstream within the nozzle,

There is still acceleration of the water in the nozzle and acceleration requires a force in the direction of that acceleration. That force must have an N3 companion. Where does that act?

On the upstream fluid, as already explained.

but the control volume experiences the acceleration within it , we should see the Resultant force in the total force calculations but we don't
There simply isn't a resultant force to the left shooting upstream as assumed.

I think the problem with these control volume examples is thru continuity P1/u1 isn't fixed it is a direct relationship to P2/u2 and A1/A2
Some supposed further upstream pressure P initial is fixed however and so is the atmosphere. P final.

In a perfectly straight pipe two things can happen when you close/attach the nozzle - either the Pinitial works harder against the resultant force downstream to keep u1 ~P1 increases or P1 P initial stays the same and u1 drops

P1,u1 will be different whether the nozzle is there or not. The resultant force of the fluid acceleration is always accounted for by the pressure difference That is frustratingly never explained in Bernoulli's

 

[Chestermiller]

Those two quantities are not the same so they can't be equated like that. The force is, of course, due to the water pressure but not just the static pressure. The fact is, there has to be an N3 pair somewhere, to explain the acceleration of the water exiting the nozzle. You have to agree that it is going faster at the tip than through the hose. If you can't address the N3 issue then you have no valid explanation.
You are right in your initial assumption about what happens when the end of the hose is blocked off (the static pressure will cause a force that could push the end off the hose or just burst it).

I stand by what I said. There is a pressure difference between the inlet and outlet of the hose, with the upstream pressure higher than the downstream pressure. Part of this pressure difference is expended in balancing the backward force exerted by the nozzle body on the fluid. The remainder of the pressure difference is used to accelerate the fluid from the low upstream velocity to the higher fluid velocity at the exit jet.

The action-reaction pair you are asking about is (a) the forward pressure force that the fluid exerts on the nozzle body and (b) the backward force exerted by the nozzle body on the fluid.

If you would like, I will develop the equations that can be used to accurately quantify the forward pressure force that the fluid exerts on the nozzle body. Please let me know if you are interested in seeing the analysis.

Chet

 

[sophiecentaur]

"Bernoulli" yes, it's not straightforward. There seem to be assumptions about the flow around a bend. The speed is not the same at different radii and that will produce pressure gradients. I am looking for a greater force on the outside of the curve but it would seem to be less according to B.

 

[Chestermiller]

Some supposed further upstream pressure P initial is fixed however and so is the atmosphere. P final.

In a perfectly straight pipe two things can happen when you close/attach the nozzle - either the Pinitial works harder against the resultant force downstream to keep u1 ~P1 increases or P1 P initial stays the same and u1 drops

P1,u1 will be different whether the nozzle is there or not. The resultant force of the fluid acceleration is always accounted for by the pressure difference That is frustratingly never explained in Bernoulli's

I am unable to fathom what you are saying here. I make you the same offer that I made to Sophiecentaur. If you desire, I will derive the equations for a nozzle attached to a straight pipe, and interpret each of the terms for you.

 

[Chestermiller]

Guys,

I think we should confine attention, at least temporarily, to a nozzle attached to a straight rigid pipe, rather than a hose. Why? If we can't analyze and reach agreement on that, we will never be able to properly consider the transient unstable undulations of a hose with a nozzle at its end.

Chet

 

[Timtam]

@Chestermiller . Yes that I think would solve the issue, as I see it we have two different scenarios ,

1 The control volume contains a constant diameter pipe 2A
2 The control volume contains a nozzle 2A to 1A

Assumptions were that the pipe is perfectly straight (so walls cannot receive a force)
The initial pressure say a pump is working constant at some fixed rate and that final pressure is atmospheric.

I am not talking about a curving hose I'm not sure how Sophie inferred Bernoullis to mean around bends instead of continuity equation

 

[Chestermiller]

Yes that I think would solve the issue, as I see it we have two different scenarios ,

1 The control volume contains a constant diameter pipe 2A
2 the control volume contains a nozzle 2A to 1A

Assumptions were that the pipe is perfectly straight so cannot receive a force
The initial pressure say a pump is working constant at some fixed rate and that final pressure is atmosphere

I am not talking about a curving hose I'm not sure how Sophie inferred Bernoullis to mean around bends instead of continuity equation

OK. I'm only going to solve item 2. Let $\dot{m}$ represent the mass flow rate and $\rho$ represent the fluid density. Let 1 represent the entry to the nozzle and 2 represent the exit from the nozzle. Then the inlet and exit velocities are:
$$v_1=\frac{\dot{m}}{\rho A_1}\tag{1}$$
$$v_2=\frac{\dot{m}}{\rho A_2}\tag{2}$$
where $A_1>A_2$.

The Bernoulli equation gives us:$$P_1+\rho \frac{v_1^2}{2}=P_2+\rho \frac{v_2^2}{2}\tag{3}$$
If we combine Eqns. 1-3, we obtain:
$$P_1-P_2=\frac{\dot{m}^2}{2\rho}\left[\frac{1}{A_2^2}-\frac{1}{A_1^2}\right]>0\tag{4}$$
The Bernoulli equation expresses the condition for conservation of mechanical energy.

Now for the control volume momentum balance on the fluid passing through the nozzle:
$$P_1A_1-P_2A_2+F=\dot{m}(v_2-v_1)\tag{5}$$where F is the forward force exerted by the nozzle body on the fluid (actually the force will be backward, so that F is negative) and the right hand side of the equation represents the rate of change of fluid momentum within the control volume. If we substitute Eqns. 1 and 2 into Eqn. 4, we obtain:$$P_1A_1-P_2A_2+F=\frac{\dot{m}^2}{\rho}\left[\frac{1}{A_2}-\frac{1}{A_1}\right]\tag{5}$$
If we combine Eqns. 4 and 5 to solve for the force F, we obtain:$$F=-\frac{(A_1-A_2)((P_1A_1+P_2A_2)}{(A_1+A_2)}\tag{6}$$
Again, this is the forward axial force exerted by the nozzle on the fluid, and it is negative, so it is acting in the direction opposite to the fluid flow. The quantity $(P_1A_1+P_2A_2)/(A_1+A_2)$ in this equation can be interpreted physically as the axial component of pressure averaged over the nozzle surface area.

The force that the fluid exerts on the nozzle body is equal and opposite to the force that the nozzle body exerts on the fluid, and is given by:$$F_F=-F=+\frac{(A_1-A_2)((P_1A_1+P_2A_2)}{(A_1+A_2)}\tag{7}$$This force acts on the nozzle in the positive flow direction.

There is also another force acting on the nozzle body from the outside. This is the effect of the gas pressure $P_2$ outside the nozzle. This force is in the negative axial direction, and is equal to $P_2(A_1-A_2)$. So the net force acting on the nozzle is given by:$$F_{net}=F_F-P_2(A_1-A_2)=\frac{(A_1-A_2)((P_1A_1+P_2A_2)}{(A_1+A_2)}-P_2(A_1-A_2)$$or
$$F_{net}=\frac{(P_1-P_2)(A_1-A_2)A_1}{(A_1+A_2)}>0\tag{8}$$
So the net force acting on the nozzle is in the positive axial direction (i.e., the direction of flow), and it is proportional to the difference between the upstream pressure and the exit pressure.

 

[Timtam]

@Chestermiller The assumption you are making is that, if exit is fixed at atmospheric, then you can change the initial pressure Px→ but the scenario I gave is a fixed inlet pressure.

Sot that's fine but you must also recognise what happens in the preceding control volume

You have a fixed inlet pressure from the pump so if you've increased the exit pressure for this preceding control volume - the flow rate must slow (against the new adverse gradient Ux -ve to that point)

This is why the comparing the two scenarios comes important as while it appears the fluid has accelerated all we have really done by adding a nozzle is slowed it and sped it back up.

In each scenario (with or without the nozzle) the flow only travels at the rate commensurate with the initial and final pressure difference . The 'real net' acceleration is fully provided by the pressure differential - This is why there is no resultant force backwards

 

[Chestermiller]

@Chestermiller The assumption you are making is that, if exit is fixed at atmospheric, then you can change the initial pressure Px→ but the scenario I gave is a fixed inlet pressure.

The analysis I presented makes no such assumption. In fact, my analysis shows is that the only important pressure parameter in this system is the inlet gauge pressure, which is equal to the difference between the inlet absolute pressure and the exit absolute pressure. You are familiar with the concept of gauge pressure, correct?

 

[Quentin_C]

The analysis I presented makes no such assumption. In fact, my analysis shows is that the only important pressure parameter in this system is the inlet gauge pressure, which is equal to the difference between the inlet absolute pressure and the exit absolute pressure. You are familiar with the concept of gauge pressure, correct?

Yes but you have used continuity to relate them. So your assuming they are related to as you have done, from the areas and velocities change by continuity . but they are fixed from the pump and the exit. The presence of the nozzle doesn't change either of these.

This is what I believe confuses many people about this scenario. It appears from the math, that there is no resultant force resulting from fluid acceleration because the analysis doesn't show the impact upstream outside the control volume.

This is why I thought it best to show derivations for both scenarios. I thought it would quite clearly show that you couldn't have the same inlet pressures and velocities between the two examples.

 

[Chestermiller]

Yes but you have used continuity to relate them. So your assuming they are related to as you have done, from the areas and velocities change by continuity . but they are fixed from the pump and the exit. The presence of the nozzle doesn't change either of these.

This is what I believe confuses many people about this scenario. It appears from the math, that there is no resultant force resulting from fluid acceleration because the analysis doesn't show the impact upstream outside the control volume.

This is why I thought it best to show derivations for both scenarios. I thought it would quite clearly show that you couldn't have the same inlet pressures and velocities between the two examples.

I have no idea what you are talking about. I stand by what I said. I guess we are just going to have to agree to disagree.

I continue to maintain that, if the inlet and outlet pressures are both fixed, the mass flow rate will have to adjust accordingly to changes in the cross sectional areas, and, as long as the inlet area is greater than the outlet area and the inlet pressure is greater than the outlet pressure, there will be a hydrodynamic resultant force on the nozzle body in the same direction as the fluid flow. This hydrodynamic resultant force will be balanced by tension in the upstream pipe.

 

[sophiecentaur]

The analysis I presented makes no such assumption. In fact, my analysis shows is that the only important pressure parameter in this system is the inlet gauge pressure, which is equal to the difference between the inlet absolute pressure and the exit absolute pressure. You are familiar with the concept of gauge pressure, correct?

OK I can buy your analysis of the straight situation and I accept that there is no 'backward force' on the nozzle. (I have a problem with the mechanics of how Equations 4 and 5 give you 6 but I guess you have been into that and that it's OK)
The OP is about a fire hose, though and the situation is always different because there is always some curvature just behind the hose; the picture of a fireman holding a hose, is pretty typical. Hoses do snake around and they need a firm hold to prevent it. That means there really is a force, even though it may not be 'backwards'. What could be causing it? Could it be the due to the centripetal force which constrains the water to move in a curve? The argument that pressure doesn't cause any backwards force would seem to transfer to a curved supply hose, which will have a straight axis, after the hose connection.

There's just one thing (a la Columbo): you can see film of people flying around on water hose jet packs. How does that work? Does the jet use air, drawn into the pack? Would the mass of air and the low velocity be enough to support a passenger (1kN force)? Is it all to do with those curved blue pipes on the pack?

 

[Chestermiller]

OK I can buy your analysis of the straight situation and I accept that there is no 'backward force' on the nozzle. (I have a problem with the mechanics of how Equations 4 and 5 give you 6 but I guess you have been into that and that it's OK)
The OP is about a fire hose, though and the situation is always different because there is always some curvature just behind the hose; the picture of a fireman holding a hose, is pretty typical. Hoses do snake around and they need a firm hold to prevent it. That means there really is a force, even though it may not be 'backwards'. What could be causing it? Could it be the due to the centripetal force which constrains the water to move in a curve?

Sure. For this to happen, the hose has to exert a higher pressure on the outside of the curve than the inside. This results in an equal and opposite force on the hose.

 

[Michael W]

Chester's equations above look correct, and I think they describe a real force, but they zero out when the area at the beginning of the nozzle is equal to the area at the end.
That violates our intuition that it would still be difficult to hold a hose with very fast moving water even if there was no area reduction.
Is our intuition wrong?
I still think sophiecentaur's instinct to use the rocket equation is correct. If you're concerned that the water is not de-compressing or chemically changing, but maintaining its density unlike rocket fuel, I agree, but I think that a similar but opposite reaction is happening at the water inlets to the pump. If the "jet pack" was fed by a submersible pump hanging from a free-floating barge, of course we would expect the barge to drift opposite the direction of the flow at the pump inlet.

 

[sophiecentaur]

Chester's equations above look correct, and I think they describe a real force, but they zero out when the area at the beginning of the nozzle is equal to the area at the end.
That violates our intuition that it would still be difficult to hold a hose with very fast moving water even if there was no area reduction.
Is our intuition wrong?
I still think sophiecentaur's instinct to use the rocket equation is correct. If you're concerned that the water is not de-compressing or chemically changing, but maintaining its density unlike rocket fuel, I agree, but I think that a similar but opposite reaction is happening at the water inlets to the pump. If the "jet pack" was fed by a submersible pump hanging from a free-floating barge, of course we would expect the barge to drift opposite the direction of the flow at the pump inlet.

Resurrecting a two year old thread - but why not?
Whatever happens to the fluid that's being pumped, the mass flow rate is conserved but the velocity can be altered in a taper (and if the fluid density changes due to Bernoulli). If the pump is in a straight line with the nozzle then there is a force 'somewhere' on the water of mv, where m is the m is flow per second and v is the velocity. The reaction force would be on the blades / pistons or whatever of the pump. I think it's important to identify which of the forces are actually relevant and also which (lateral) forces 'cancel out'. But Newton 3 must always apply or all our lives could change.

 

[Chestermiller]

Chester's equations above look correct, and I think they describe a real force, but they zero out when the area at the beginning of the nozzle is equal to the area at the end.
That violates our intuition that it would still be difficult to hold a hose with very fast moving water even if there was no area reduction.
Is our intuition wrong?
I still think sophiecentaur's instinct to use the rocket equation is correct. If you're concerned that the water is not de-compressing or chemically changing, but maintaining its density unlike rocket fuel, I agree, but I think that a similar but opposite reaction is happening at the water inlets to the pump. If the "jet pack" was fed by a submersible pump hanging from a free-floating barge, of course we would expect the barge to drift opposite the direction of the flow at the pump inlet.

If the area at the beginning and end of the nozzle is the same, then you basically have a straight pipe in static equilibrium, with a fluid flowing at constant velocity through it. So let's consider the forces acting on the pipe. What force is the atmosphere exerting on the very exit end of the pipe (exposed to the air)? What is the nature of the horizontal force that the flowing fluid exerts on the inside surface of the pipe (assuming that the fluid is not totally inviscid)? What direction is this force acting?

 

[gmax137]

I did some googling on fire hose nozzle reactions. Here's a link
https://www.fireengineering.com/articles/print/volume-159/issue-4/features/measuring-and-demonstrating-nozzle-reaction.html

it shows a measurement of reaction force using a fish scale

 

[Chestermiller]

I did some googling on fire hose nozzle reactions. Here's a link
https://www.fireengineering.com/articles/print/volume-159/issue-4/features/measuring-and-demonstrating-nozzle-reaction.html

it shows a measurement of reaction force using a fish scale

View attachment 234858

In this photo, the hose is obviously curved, which is the reason for a constraining force to be needed. If the hose were perfectly straight, no such force would be required.

 

[sophiecentaur]

This discussion is reminding me strongly of the 'how does an aeroplane fly?' question. There are the bigendians who say it's because of Beernoilli and the littleendians who say it's because of Newton's Third Law.
But, whatever calculations that the bigendians introduce, there is no way that a plane flies because of a reaction less force. Similarly, with the fireman's hose, there has to be a reaction force but where it applies and what other forces are involved is a rich source of ideas and disagreements. For a hose with a vertical curve, the lateral forces will balance. For an in-line short hose and pump, there will be a force on the back of the pump. If the hose has an S in it then there will be forces on the 'back' internal face of the hose and possibly some force still on the pump itself. This will constitute a couple which will cause the hose to snake up and down. The centripetal force on the water flowing round the curve can also be relevant. If there is any deviation from straightness of hose, there will be some component of force on it that is partly balancing the Impulse force on the ejected water.

 

[sophiecentaur]

What direction is this force acting?

The net force backwards has to be the same as the force propelling the water. There will be a component of force in the line of the nozzle on every internal part of the water system. Many of these forces within the water path will cancel (as with symmetrical tapers). In particular, as a nozzle will be tapered from the wide hose to the narrow outlet, that resultant force there will be forwards, If you take the simplest form of pump, it could be a simple piston in a very long cylinder. If cylinder and hose are the same diameter and everything is straight in line, up to the nozzle taper, the reaction force on the piston will be the same as the propulsive force on the emerging water plus the forward component of the force on the taper. Other tapers and bends will introduce more forces in the system.

 

[Chestermiller]

The net force backwards has to be the same as the force propelling the water.

Actually, in a straight pipe of constant cross section, the only force interaction between the flowing fluid and the pipe (in the horizontal direction) is the frictional drag at the wall. The wall exerts a viscous shear stress in the negative flow direction on the fluid, and the fluid exerts an equal and opposite viscous shear stress in the positive flow direction on the inner wall of the pipe.

If the fluid were inviscid, there would be no horizontal force interaction between the straight pipe and the fluid at all. The fluid would just be traveling down the pipe at constant velocity, and, since it is not accelerating, no forces would be needed to maintain this. The only forces that would come into play in this kind of inviscid flow situation would be if there were curvature to the pipe. Such forces would be necessary to change the direction of the flowing fluid. We are all familiar with the inertial forces between a flowing fluid and the pipe when 90 degree and 180 degree bends are involved. In such cases, the pipe would have to be properly supported.

 

[sophiecentaur]

Actually, in a straight pipe of constant cross section, the only force interaction between the flowing fluid and the pipe (in the horizontal direction) is the frictional drag at the wall.

I have a feeling that we are talking slightly in quadrature here. Have I missed bit where you consider the reaction force that I am batting on about?
I have no problem with the detail of what you are saying but a 'complete' explanation must include a Newton3 reaction force against 'something', which will usually have contributions at many different points. If the hose is curved then there is some force component from the 'outside face' of the curve.
The friction forces you introduced are internal and will be balanced by other internal forces such as tension in the hose and forces in the pump. (And in bends, as you say).
But the ejected water has gained Momentum and that must have had forces on it during its passage through the system. Forget the water supply pipe and replace it with a large tank of water and you can say the initial velocity is zero. The accelerating forces must be acting, ultimately, either as a force against the Earth or a rocket-like force to accelerate the pump equipment.
The water jet harness, mentioned earlier, is an extreme case where a reaction force on the upper face of the hose loop provides the force to support the driver.

 

[CWatters]

Would be interesting to consider a straight rigid but telescopic pipe with a tapered nozzle...

When you turn the water on does it..

a) extend (due to pressure on the inside of the nozzle) or
b) retract (due to the water accelerating through the nozzle and conservation of momentum)
c) remain at constant length
d) both effects a) and b) exist but one is greater?

 

[jbriggs444]

Would be interesting to consider a straight rigid but telescopic pipe with a tapered nozzle...

When you turn the water on does it..

a) extend (due to pressure on the inside of the nozzle) or
b) retract (due to the water accelerating through the nozzle and conservation of momentum)
c) remain at constant length
d) both effects a) and b) exist but one is greater?

Seems quite obvious. There are only two forces involved in the interaction between nozzle and water: pressure and viscous friction. Both act to push the nozzle in the direction of flow. There are only two forces involved in the interaction between the telescoping pipe walls and the water: pressure and viscous friction. The former has no effect in the direction of the flow. The latter acts to drag the pipe in the direction of the flow.

One end of the pipe+nozzle is anchored to the tap. The other end is free. The net horizontal force on nozzle plus pipe causes them to extend away from the tap. So the nozzle and pipe extend when you turn on the valve.

If we include gravity and assume a horizontal pipe, there is a vertical pressure gradient which acts to compensate for it and keeps the flow horizontal.

Given a freely telescoping pipe and nozzle with negligible mass and unlimited extent, the egress flow rate is also negligible. The pipe extends out almost as fast as water comes in and only a dribble actually comes out of the nozzle. We may have to consider an equilibrium condition involving air resistance on the rapidly extending pipe.

Edit: the usual deployment is in a vertical orientation on a timer so that the pop-up watering nozzles can irrigate one's lawn. (Though the flow diverter at the nozzle makes this less than an ideal example).

 

[russ_watters]

This discussion is reminding me strongly of the 'how does an aeroplane fly?' question. There are the bigendians who say it's because of Beernoilli and the littleendians who say it's because of Newton's Third Law.
But, whatever calculations that the bigendians introduce, there is no way that a plane flies because of a reaction less force. Similarly, with the fireman's hose, there has to be a reaction force but where it applies and what other forces are involved is a rich source of ideas and disagreements.

I kind of agree from a science standpoint, but the main problem with these threads is that many people are not answering the question being asked.

My speculation on why is that when one points out that the firefighter is holding onto the hose, leaning forward and asks why, it triggers an analysis of what the water is doing to the nozzle, and a set of blinders that obscures the original question. Conclusion: the water is pushing the nozzle forward. But the question being asked is not "what is the direction fo the force the water is applying to the nozzle?", the question is "what force is pushing the firefighter backwards?"

The exact numerical answer is dependent on the setup and assumptions (as always), but the answer will be a combination of one or more of the following (in no particular order):

1. The elasticity of the hose.
2. The static pressure of the water in the hose.
3. The momentum of the water entering and exiting the hose.

In addition, it is notable that for some scenarios the firefighter is indeed being pushed forwards, not backwards. That's interesting, but not what is generally being asked about.

Speaking of backwards, I think a lot of the reason for the rhetorical problem in these threads is that they are in fact backwards. Most of what we do here is homework help and for most such problems, the scenario is clearly defined and you calculate what happens. But this thread starts with what happens and asks why. Then immediately, people construct a scenario, calculate a correct answer for their own scenario and never go back to check if that answers the OP's question. Many construct the wrong scenario and as such answer the OP's question wrong.

 

[sophiecentaur]

I kind of agree from a science standpoint, but the main problem with these threads is that many people are not answering the question being asked.

Not for the first time on PF, i think.
I like your post. The original question is hiding a paradox / misconception in people's intuition. The OP gives two apparently opposing ideas when they are actually not mutually exclusive. A narrowing taper will produce a forwards force on the hose but there are other forces at work, which can push / pull firefighters in many directions - including backwards. It's not surprising that there's confusion because we all know about rockets. But a bit of thought will remind us that rocket engines tend to have an widening taper and not a narrowing one. N3 comes along and he has to be right. The perfect storm for a PF thread.

The action-reaction pair you are asking about is (a) the forward pressure force that the fluid exerts on the nozzle body and (b) the backward force exerted by the nozzle body on the fluid.

Not that pair; there are any number of pairs that could be considered and I am considering the overall forces on the whole pump / hose / nozzle kit, due to the expelled water. I realize that half of the OP content asks about the force on the nozzle (the one you correctly refer to and deal with) but also the op asks for an explanation of the forces on the firefighter. I'm talking about the force that must have existed to accelerate the fluid out of the nozzle and the necessary N3 force must act on a number of parts of the restraint of the system. Whenever Momentum is changing, there will be a force and a curve on the hose is one example. The fighter needs to minimise that force or at least make sure that it's in a controllable direction (down towards the ground and not sideways or up).
I cannot see how people still seem to be ignoring the need for the overall N3 constraint. As I said above - this is just like the flying aircraft wing discussions. Both approaches are valid as far as they go.

 

[sophiecentaur]

Though the flow diverter at the nozzle makes this less than an ideal example).

I just spotted this on re-reading. If you mean by "flow diverter", a mechanism for spreading the water around, then a rotary flow diverter (Catherine wheel style) follows exactly my explanation for the fire hose. The reaction against the force on the departing water causes the arm on the end to spin in the opposite direction.

 

[glennr]

An old thread, but this is relevant:

https://link.springer.com/article/10.1007/s10694-014-0430-5

 

[cjl]

Not for the first time on PF, i think.
I like your post. The original question is hiding a paradox / misconception in people's intuition. The OP gives two apparently opposing ideas when they are actually not mutually exclusive. A narrowing taper will produce a forwards force on the hose but there are other forces at work, which can push / pull firefighters in many directions - including backwards. It's not surprising that there's confusion because we all know about rockets. But a bit of thought will remind us that rocket engines tend to have an widening taper and not a narrowing one. N3 comes along and he has to be right. The perfect storm for a PF thread.

The rocket nozzle is expanding because that is the way to achieve the highest exhaust velocity. Supersonic flows behave inversely to subsonic flows when it comes to changes in flow area, so expansion increases velocity and contraction decreases it. This is not necessary to generate thrust though. A rocket with a convergent-only nozzle would still produce a very considerable amount of thrust. Indeed, this is frequently the case on jet engines.

Not that pair; there are any number of pairs that could be considered and I am considering the overall forces on the whole pump / hose / nozzle kit, due to the expelled water. I realize that half of the OP content asks about the force on the nozzle (the one you correctly refer to and deal with) but also the op asks for an explanation of the forces on the firefighter. I'm talking about the force that must have existed to accelerate the fluid out of the nozzle and the necessary N3 force must act on a number of parts of the restraint of the system. Whenever Momentum is changing, there will be a force and a curve on the hose is one example. The fighter needs to minimise that force or at least make sure that it's in a controllable direction (down towards the ground and not sideways or up).
I cannot see how people still seem to be ignoring the need for the overall N3 constraint. As I said above - this is just like the flying aircraft wing discussions. Both approaches are valid as far as they go.

The overall N3 constraint isn't ignored, but it can be somewhat nonintuitive. In the case of a completely straight pipe/hose with a nozzle on the end, the only force acting on the entire pipe/nozzle system will be in the same direction as the flow. The N3 reaction force from the fact that the water is coming out the end will only be felt in the backwards force exerted on the pump itself (which can alternatively be seen as the force caused by the pressure differential between the pump inlet and outlet). For your water tank example, there's a slight force on the tank itself caused by the fact that the opening out of which the water is flowing is an opening, and thus, the water is not exerting hydrostatic pressure on the tank at that point. There's an imbalance because on one side of the water tank, the water is pushing against a region that is not mirrored on the other side due to the opening. As such, the tank will experience a force away from the direction of the outlet.

(I realize this is now the second time this has been resurrected, but it felt like it had never really come to a satisfactory answer, so hopefully this is helpful)

 

[sophiecentaur]

The rocket nozzle is expanding because that is the way to achieve the highest exhaust velocity.

I would say that, because of Bernouli, the pressure after the constriction goes up and the gas speed drops. But that doesn't actually go against what you say because the combustion conditions are optimised.

There's an imbalance because on one side of the water tank, the water is pushing against a region that is not mirrored on the other side due to the opening. As such, the tank will experience a force away from the direction of the outlet.

I agree that looking for N3 involves looking everywhere. People only want to look at the nozzle and that accounts for the wrong thinking that we read about.

 

[cjl]

I would say that, because of Bernouli, the pressure after the constriction goes up and the gas speed drops. But that doesn't actually go against what you say because the combustion conditions are optimised.

This is false. After the constriction, the speed rises dramatically (and the pressure continues to drop). Bernoulli is not applicable. For a fairly common rocket nozzle where the exit pressure is 1/125 of chamber pressure (so, for example, an exit pressure of 10 PSI and a chamber at 1250, which corresponds to an area expansion ratio of just under 10:1), the mach number at the exit will be 3.85, and the exhaust velocity will be 2.12 times higher than the velocity in the throat.

The reason bernoulli (and a lot of common sense about how fluids behave in general) doesn't apply is because of the compressibility of the flow. In compressible flows, a constriction only accelerates a flow if the flow is subsonic. Once you hit a mach number of 1, you actually have to expand the flow to continue accelerating it. The pressure drop as the flow accelerates is so dramatic that the volumetric flow rate is increasing faster than the linear flow rate is (due to the drop in density of the gas as the pressure falls), so a converging-diverging nozzle is actually the best way to achieve maximum exhaust velocity when you have a large pressure gradient across the nozzle (and your working fluid is compressible).

 

[sophiecentaur]

The reason bernoulli (and a lot of common sense about how fluids behave in general) doesn't apply is because of the compressibility of the flow. In compressible flows, a constriction only accelerates a flow if the flow is subsonic.

Brilliant - thanks for that.