Sumedh
- 61
- 0
Homework Statement
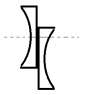
A biconvex symmetrical lens is cut in two halves and placed as shown in figure.
if a point object is placed in the left how many images will be formed
options - (a) Two images
(b) Three images
Homework Equations
The Attempt at a Solution
As I have used the lens makers formula the focal length of upper part and lower part is same
so they will form images that coincides and hence one image will be formed and the other image will be formed by the middle (thick overlapping part)
so finally 2 images will be formed.
but the answer that is given in my book is (b)Three images will be formed.
I will be very thankful even if hints are provided.