ch2kb0x
- 31
- 0
Homework Statement
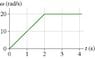
There is an attachment for the picture. question is, How many revolutions does the object make during the first 4 s?
Homework Equations
The Attempt at a Solution
I attempted to solve this by dividing 20 by 2pi, but apparently, that was wrong. Any help?