On the motion of a particle on the inner surface of a sphere

[gnits]

Homework Statement

Determination of the motion of a particle on the inner surface of a sphere

Relevant Equations

F = mv^2/r

Could anyone please help me out with the second part of this question:

I've got the first part, u = √(5ga)

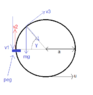
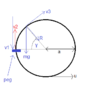
Here's my diagram for the second part:

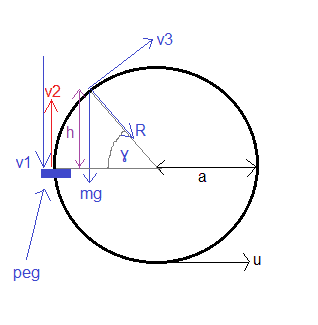
Distance traveled is from bottom of sphere to peg is 2πa/3 which means angle traveled is 2π/3.

So the particlee is going to travel 2π/3 radians and then hit the peg with velocity v1. It will rebound with velocity v2 after that will have a general position with velocity v3 and normal reaction R.

So, equating energy at start of motion at bottom of sphere with that at arrival at the peg we have:

½ m u^2 = ½ m v1^2 + mga

This rearranges to give:

v1 = √(u^2-2ga)

and as coefficient of restitution = ½ we then have:

v2 = ½ √(u^2-2ga)

So now, equate energy just after rebound with energy in general position to get:

½ m * ¼(u^2-2ga) = ½ m v3^2 + mga sin(ϒ)

This rearranges to give:

v3^2 = u^2/4 + ga/2 - 2ga sin(ϒ)

Now, centripetal force at general position is given by:

R + mg sin(ϒ) = m*v3^2/a

Substitute in for v3^2 from prior equation to get

R + mg sin(ϒ) = mu^2/4a + mg/2 - 2gma sin(ϒ)

Now we set R = 0 (this will be where the particle looses contact with the surface), then cancel through by m and substitute in that u = √(5ga) to get:

3g sin(ϒ) = 7g/4

This leads to sin(ϒ) = 7/12 = h / a and so

h = 7a/12 which would give an answer of 7a/12 + a = 19a/12

BUT the book asnwer is 5a/4

Thanks for any help,
Mitch.

 

[TSny]

½ m * ¼(u^2-2ga) = ½ m v3^2 + mga sin(ϒ)

This rearranges to give:

v3^2 = u^2/4 + ga/2 - 2ga sin(ϒ)

Check the signs of the terms on the right side of the second equation above.

 

[gnits]

Thanks very much TSny. I must have read and reread this error of sign every time I checked and rechecked. Indeed the answer then agrees with the books. Thanks very much.