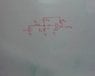OP AMP Transfer Function Homework: Find Vo(s)/Vi(s) for Circuit

[clope023]

Homework Statement

Find Vo(s)/Vi(s) for the OPAMP circuit in the attachements

Homework Equations

V = iR, Kirchoff current law.
1/sC = Laplace transform of capacitor impedance.

The Attempt at a Solution

Make the voltage at the node = v'.

ir1 = (vi - v')/r1
ir2 = v'/r2
iz = (v'-vo)/z
z = (1/sC1)+r3
ic2 = (v'-v-)/(1/sC2)

Op amp inverting pin does not draw current and due to the virtual ground v-=0V
Therefore,

ir1 = ir2 + ic2 + iz

\frac{vi-v'}{r1} = \frac{v'}{r2} + sC2v' + \frac{v'-vo}{(1/sC1)+r3}

Ideally I would do the algebra and solve for the transfer fuction by setting vo/vi to whatever what came out on the other side, what I am having trouble with is canceling out v', which I attempted to write as a multiple of either vi or vo via a voltage divider.

My attempts were as follows:

v' as a function of vi -

v' = \frac{R2vi}{R1+R2}

or v' as a function of vo -

v' = \frac{R2vo}{(1/sC2)+R3 + R2}

I'm just wondering which way of thinking in terms of v' is the right way to go, I keep on getting all of these horribly long equations that just don't seem right so I decided to ask on here, any help is greatly appreciated.

 

[gneill]

I think you've interchanged the roles of capacitors C1 and C2 between your diagram and equations. Just thought you'd like to know.

If you just want results for an ideal op-amp, you won't go far wrong by simply taking v' to be zero. That is, consider it a pseudo-ground for the small ac signal case. This is so because the op-amp is going to do its darndest to make the current flowing through the capacitor on the input leg zero. To do that, the feedback loop has to drive the v' node towards ground and hold it there. Even on a "real" op-amp the input current going through the input capacitor will be on the order of picoamps.

Of course, that also means that your R2 won't be doing much either. Your input current will be Vi/R1, and that current will carry on through the feedback components to arrive at Vout.

If you've got a few hours to kill doing complex algebra you could always replace the op-amp in the circuit with an equivalent circuit model and solve via mesh analysis.

 

[The Electrician]

Check your schematic for correctness. If the opamp is ideal, then C1 does nothing in the small signal response (because the input impedance of the minus input is infinite), and blocks any path for the DC bias current which must be provided to the minus input.