Optimizing Light Pole Height for Maximum Illumination: A Differential Problem

[Bob777]

Homework Statement

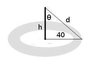
A light is to be placed atop a pole of height h feet to illuminate a busy traffic circle, which has a radius of 40ft. The intensity of illumination I at any point P on the circle is directly proportional to the cosine of the angle θ (see the figure) and inversely proportional to the square of the distance d from the source.
(a)How tall should the light pole be to maximize I?

Homework Equations

The Attempt at a Solution

intensity of illumination I=cosθ/d^2
cosθ/d^2*the area=I
but any point P has different intensity of illumination according to the distance form center.
and when h change all the intensity of illumination of any point change.
How can I know the I?

Please help me! thanks

 

[sunjin09]

write d as a function of θ, which seems straightforward, then I=cosθ/d(θ)^2, now you can take the derivative

 

[Bob777]

write d as a function of θ, which seems straightforward, then I=cosθ/d(θ)^2, now you can take the derivative

not I =cosθ/d(θ)^2.
It's "intensity of I"
"intensity of I"=cosθ/d(θ)^2

points have different θ with different radius.
and when h changes everything changes.

:-(

 

[sunjin09]

The intensity you want to maximize is cosθ/d(θ)^2, which is a function of θ, you want to choose a θ, so that this intensity is maximized. How do you choose θ? You realize that when the intensity is maximized, its derivative with respect to θ is zero... now try to work out the rest. Regarding h, think of h changes with θ, not the contrary

 

[Bob777]

The intensity you want to maximize is cosθ/d(θ)^2, which is a function of θ, you want to choose a θ, so that this intensity is maximized. How do you choose θ? You realize that when the intensity is maximized, its derivative with respect to θ is zero... now try to work out the rest. Regarding h, think of h changes with θ, not the contrary

Thank you very much for your reply. :)

My question is that the intensity is different at different points on the circle.
I don't know which point on circle it's intensity I have to find the h to maximize .
Should I find maxim intensity of all points on the circle?

 

[HallsofIvy]

Thank you very much for your reply. :)

My question is that the intensity is different at different points on the circle.

The intensity depends only upon the strength of the light itself and the distance to the light. Those are the same for every point on each circle. The intensity is NOT "different at different points on the circle". That's the whole point of using those circles to analyse the problem.

I don't know which point on circle it's intensity I have to find the h to maximize .
Should I find maxim intensity of all points on the circle?

 

[Bob777]

The intensity depends only upon the strength of the light itself and the distance to the light. Those are the same for every point on each circle. The intensity is NOT "different at different points on the circle". That's the whole point of using those circles to analyse the problem.

Thank you very much!

Now there is no problem.

:-)