Optimizing Resultant Forces: Finding Maximum and Minimum Magnitudes

[Needhelp2]

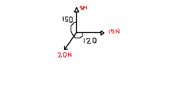
Three horizontal forces of magnitudes 8N, 15N and 20N act at a point. The 8N and 15N are at right angles to each other. The force 20N makes an angle of 150 degrees with the the 8N force and an angle of 120 degrees with the 15N force.

State the greatest and least possible magnitudes of the resultant force if the directions of the three horizontal forces can be altered.

Any help would be greatly appreciated, the question had many parts, the last one ( the one above) threw me (Nerd)
Thank you!

sorry for the poor diagram!

 

[Jameson]

I believe that the greatest magnitude will be when they all have the same direction and the minimum magnitude will be when two are in one direction and the third is in the opposite. This can be demonstrated visually by head to tail addition. I know this is true for two vectors and I don't see why it shouldn't apply to three.

 

[Ackbach]

I believe that the greatest magnitude will be when they all have the same direction and the minimum magnitude will be when two are in one direction and the third is in the opposite. This can be demonstrated visually by head to tail addition. I know this is true for two vectors and I don't see why it shouldn't apply to three.

[EDIT] This post is completely wrong, as shown by Opalg's post below. Please disregard.

You can actually get a zero magnitude resultant vector in a fairly straightforward manner, at least in this problem. Solution: put the 20N force going straight left, and the 15N force going straight right. Then put the 8N force at an angle such that its x-component is +5. You can use the inverse cosine function to find out what angle that will be (there are actually two solutions, of course). Since you can't get a negative magnitude for the resultant vector, this will be the minimum.

 

[Opalg]

View attachment 162
To get the forces in equilibrium (so that the resultant force has zero magnitude), arrange their directions so as to form a closed triangle, as in the diagram.

 

[Needhelp2]

Thank you so much! It came up in my Mechanics mock, so the fact I couldn't do it worried me slightly... But the simple solution makes me feel a bit better :)