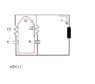
- #1
Tach
- 6
- 0
Let's say you have two batteries in parallel and at the same voltage. Well batteries fluctuate in voltage and when they are drained they will have a somewhat lower voltage than what they started with when fully charged. Because of this, when power (or current rather) is being drawn from a battery into a circuit (or load if you will), the battery with the slightly higher voltage will supply energy (current) to the circuit (load) until its voltage level is at an equal or lower level than the other battery voltage? From which the other battery will then be supplying the energy (current) to the circuit (load)? Is this correct?
I guess theoretically while one battery is at a higher voltage level there will be a small current going across the other battery, so a parallel setup would be considered less than ideal if given a choice between series, in general.
But I'm asking this because I'm come up with a dilemma regarding this setup in a solar regulating circuit and I want to make sure this is what is going on. Any replies or help in understanding is greatly appreciated.
I hope I was adequately clear.
I guess theoretically while one battery is at a higher voltage level there will be a small current going across the other battery, so a parallel setup would be considered less than ideal if given a choice between series, in general.
But I'm asking this because I'm come up with a dilemma regarding this setup in a solar regulating circuit and I want to make sure this is what is going on. Any replies or help in understanding is greatly appreciated.
I hope I was adequately clear.