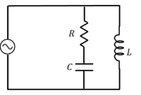
lys04 said:
By the way the solutions look like this
View attachment 352416
It's much more clear on log-log plot, which is standard. That way you will get straight line asymptotes for an approximate solution. Pro EEs will call the vertical axis dBΩ, which is ##20*log(|Z|)##, the phase is plotted as degrees, both with either a ##log(\omega)## or ##log(f)## horizontal axis.
You will want to keep your transfer function in a factored pole-zero form where you have linear ##(1+\frac{ j \omega}{\omega_n})##, or quadratic ##(1+(\frac{1}{Q})(\frac{ j \omega}{\omega_n}) + (\frac{ j \omega}{\omega_n})^2)## terms. These will typically be separated in frequency and can thus be treated independently in the plotting process.
The correct (intuitive) way is really a lot to explain here, but look for this book online (I can't link to it here). It has a good description of manual frequency response (bode) plotting in section 8. You can pretty much ignore most all of the previous comments (sorry guys, I call them like I see them). Your original formula for Z in post #1 is all you need. Further arithmetic will just obscure things. You want the polynomial factors of ##j \omega##, not the expanded polynomial. Do not simplify ##(j \omega)^2 = -\omega^2##, even though that's true. That's great for a calculator, but not a good approach for understanding the system dynamics.

Finally, there is a big advantage to learning how to do this by hand for analog EEs. Even though your data lives in a computer that can calculate and plot things for you, you won't get a good understanding of what a pole, zero, or quadratic term really does to the frequency response of your system. It's similar to learning in your algebra class to solve quadratic equations even though Wolfram-Alpha et. al. can do it for you.
P.S. - In that book, as well as most other analog EE texts, you will see polynomials in ##s##. For your case you can use ##s=j \omega##, which is true for steady state solutions. You'll learn why people do this later (hint: Laplace Transforms).