Parallel/Series Circuit w/ Capacitors

  • Thread starter Thread starter littlebilly91
  • Start date Start date
  • Tags Tags
    Capacitors Circuit
AI Thread Summary
The discussion focuses on understanding how the arrangement of capacitors in a circuit affects their equivalent capacitance, particularly when a horizontal line with an arrow is present. It clarifies that capacitors are in parallel if their terminals connect to the same two nodes, resulting in the same voltage across them. The presence of the horizontal line complicates the identification of series and parallel configurations. The conversation highlights the importance of recognizing the number of nodes in the circuit for accurate analysis. Overall, the arrangement of capacitors significantly impacts their equivalent capacitance calculations.
littlebilly91
Messages
21
Reaction score
0
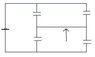
I am doing a problem about equivalent capacitors and I am not sure how I should handle this arrangement. How does the horizontal line (with the arrow) change whether the capacitors are in series or parallel? I know without that line you can condense the pairs of capacitors as if they were in series and then take those two equivalent capacitors are wired in parallel, but the horizontal line does complicate things a bit.
Thanks.
 

Attachments

  • cap.jpg
    cap.jpg
    3 KB · Views: 389
Physics news on Phys.org
Two loads are in parallel if their terminals connected to the same two nodes ( they have the same voltage across the terminals)

Hence, there are 3 nodes in this circuit
 
Oh, i never looked at it like that, thanks a lot
 

Thread 'Errors and significant figures'

I multiplied the values first without the error limit. Got 19.38. rounded it off to 2 significant figures since the given data has 2 significant figures. So = 19. For error I used the above formula. It comes out about 1.48. Now my question is. Should I write the answer as 19±1.5 (rounding 1.48 to 2 significant figures) OR should I write it as 19±1. So in short, should the error have same number of significant figures as the mean value or should it have the same number of decimal places as...
View full post »
Thread 'A cylinder connected to a hanging mass'

Thread 'A cylinder connected to a hanging mass'

Let's declare that for the cylinder, mass = M = 10 kg Radius = R = 4 m For the wall and the floor, Friction coeff = ##\mu## = 0.5 For the hanging mass, mass = m = 11 kg First, we divide the force according to their respective plane (x and y thing, correct me if I'm wrong) and according to which, cylinder or the hanging mass, they're working on. Force on the hanging mass $$mg - T = ma$$ Force(Cylinder) on y $$N_f + f_w - Mg = 0$$ Force(Cylinder) on x $$T + f_f - N_w = Ma$$ There's also...
View full post »

Similar threads

Why Do Capacitors Behave Differently in Series and Parallel Configurations?
Replies
20
Views
2K
Why Capacitors in Parallels vs. Series: Coaxial Capacitor Case
Replies
2
Views
2K
Questions about a capacitor with 4 parallel plates
Replies
14
Views
1K
How Do You Calculate Capacitance in a DC Circuit with a Fully Charged Capacitor?
Replies
3
Views
1K
How to determine if electrical components are connected in parallel or in series?
Replies
10
Views
903
A circuit with switches, capacitators and resistors
Replies
6
Views
2K
Capacitance of a circular capacitor with two parallel dielectrics
Replies
2
Views
1K
Capacitor Questions Charging and Discharging
Replies
4
Views
3K
Equivalent capacitance of circuit
Replies
12
Views
7K
Series RLC and Parallel RLC circuits
Replies
15
Views
5K

Hot Threads

Recent Insights

Back
Top