TESL@
- 122
- 8
Hello,
I am currently trying to parametrize a surface constructed by thickening a rather complicated curve, defining its normal, binormal and tangent vectors. Even using Mathematica simplification, the resulting vectors are page long expressions and the reason for it is because I have four additional variables in the position vector equation aside from the parameter itself.
I cannot post what I get after computing the vectors because it is too long to make sense but my curve is a torus knot, and it obviously depends on the torus surface on which it dwells, thus its radii (r and R) and the knot integers (p and q). These are the four variables.
What would you recommend to simplify the process? I cannot assign numerical values to these variables since I will have to change them later, so do I have to deal with the original equations or is there a method to somehow group all the variables together?
Thank you.
edit: This is the curve equation. Things get a lot worse after taking the derivative of the normalized tangent vector.
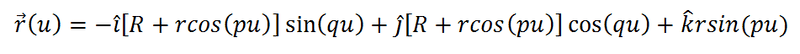
edit2: Here is an applet visualizing what I am doing. It provides the code but I cannot see how it is defined mathematically.
http://demonstrations.wolfram.com/TorusPaths/
By the way, any idea is appreciated since I have limited time. Thank you.
I am currently trying to parametrize a surface constructed by thickening a rather complicated curve, defining its normal, binormal and tangent vectors. Even using Mathematica simplification, the resulting vectors are page long expressions and the reason for it is because I have four additional variables in the position vector equation aside from the parameter itself.
I cannot post what I get after computing the vectors because it is too long to make sense but my curve is a torus knot, and it obviously depends on the torus surface on which it dwells, thus its radii (r and R) and the knot integers (p and q). These are the four variables.
What would you recommend to simplify the process? I cannot assign numerical values to these variables since I will have to change them later, so do I have to deal with the original equations or is there a method to somehow group all the variables together?
Thank you.
edit: This is the curve equation. Things get a lot worse after taking the derivative of the normalized tangent vector.
edit2: Here is an applet visualizing what I am doing. It provides the code but I cannot see how it is defined mathematically.
http://demonstrations.wolfram.com/TorusPaths/
By the way, any idea is appreciated since I have limited time. Thank you.
Last edited: