postechsung
- 3
- 1
- Homework Statement
- Particle in a box
- Relevant Equations
- Schrodinger Eq
Hi, I'm trying to prove a wave equation of particle in a box situation.
In many solutions, they used a equation like Eq = Asin(kx)+Bcos(kx).
Instead, I want to prove using Eq = Aexp(ikx) + Bexp(-ikx).
So, this is my solution.
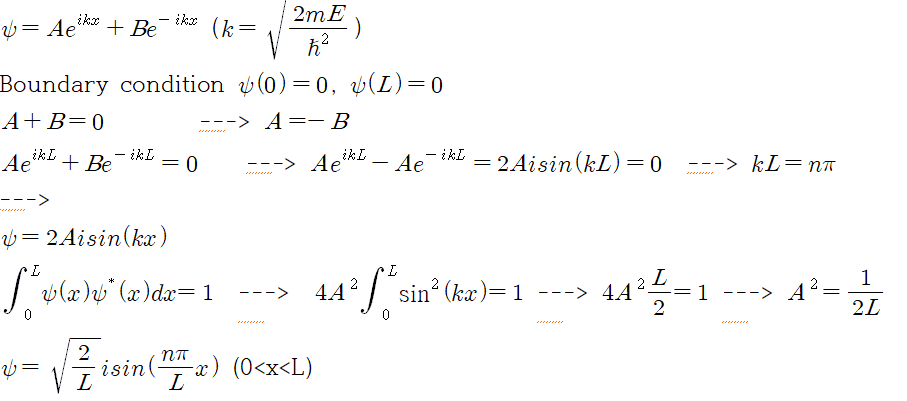
However, the original (well-known) solution is without i. (psi = sqrt(2/L) sin(n pi x/L)
Is two wave function is same? or is there any error in my solution?
Sorry for my bad English. I'm new to here and looking forward to get help.
THANKS!
In many solutions, they used a equation like Eq = Asin(kx)+Bcos(kx).
Instead, I want to prove using Eq = Aexp(ikx) + Bexp(-ikx).
So, this is my solution.
However, the original (well-known) solution is without i. (psi = sqrt(2/L) sin(n pi x/L)
Is two wave function is same? or is there any error in my solution?
Sorry for my bad English. I'm new to here and looking forward to get help.
THANKS!