Particle motion + electric field when voltage varies

[RmsAdd]

Homework Statement

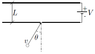
Two parallel plates located at a distance "L" from each other they maintain a potential difference "V" because of a battery (as shown in the picture). Through a small hole, made in bottom plate, electrons get into system (with mass "m" and charge "-e"), with velocity "v" and forming a θ angle with the perpendicular direction of the plate. A flourescent screen at the top plate allows to determine where the electrons impact.

If there is a small change dV at the potential difference betwen the plates. Where and how much the position where electrons impact varies? (Do not matter about relativism effects and cuatic effects). Make a scheme about the dependency of that variation with the velocity v and the angle θ.

Spoiler: Original problem statement (Spanish)

Dos placas paralelas situadas a distancia L una de la otra, se mantienen a una diferencia de potencial V por medio de una batería, como muestra la figura. Por un pequeño orificio practicado en la placa de abajo ingresan electrones (de masa m y carga -e), con una velocidad v y formando un angulo θ con la dirección perpendicular a la placa. Una pantalla fluorescente en la placa de arriba permite determinar dónde inciden los electrones.
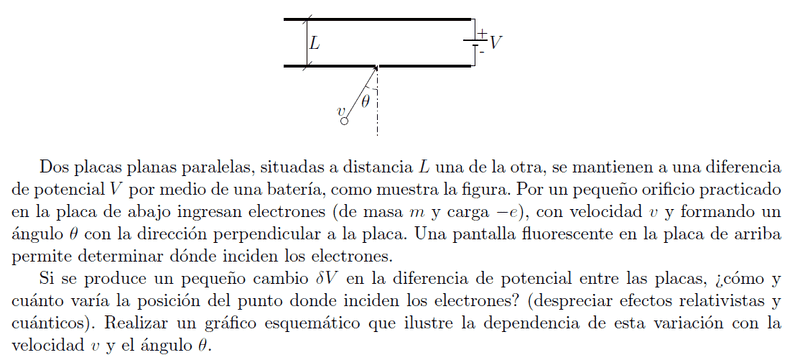
Si se produce un pequeño cambio dV en la diferencia de potencial entre las placas, ¿Cómo y cuanto varía la posición donde inciden los electones? (despreciar efectos relativistas y cuánticos). Realizar un grafico esquematico que ilustre la dependencia de esta variación con la velocidad v y el angulo θ

Homework Equations

The Attempt at a Solution

Energy analisis:

The initial energy and the final energy have to be the same.
$$E_{f}=E{i}$$
$$E_{kf}=E_{ki}+U_{e}$$
$$\frac12 \cdot m \cdot v_{f}^{2}=\frac12 \cdot m \cdot v_{i}^{2}+F_{e} \cdot L$$
$$v_{f}=\sqrt{ v_{i}^{2}+ \frac{2 \cdot F_{e} \cdot L}{m}}\qquad \text{(1)}$$

Motion analisis:

$$\Sigma F_{x}=0$$
$$v_{x}=constant$$
$$\Sigma F_{y}=m \cdot \vec{a}$$

So we have a constant uniform motion in x-axis and a constant aceleration in y-axis. I can find the final velocity in y-axis using Pythagorean teorem

$$v_{f}^2=v_x^2 + v_{fy}^2$$
$$v_{fy}=\sqrt{v_f^2 - v_x^2}$$

In y-axis aceleration is constant so I can do:
$$V_{m}=\frac{v_{fy}+v_{iy}}{2}$$
$$V_{m}=\frac{\Delta y}{\Delta t}$$
$$\Delta t=\frac{2 \Delta y}{v_{fy}+v_{iy}} \qquad \text{(2)}$$
This is the time that it takes to the particle in order to reach the top plate. I can use $\Delta t$ to get x-axis distance.
$$v_x=\frac{\Delta x}{\Delta t}$$
$$x=v_x \cdot \Delta t$$

Replacing with (2):
$$x=v_x \cdot \frac{2 \Delta y}{v_{fy}+v_{iy}}$$
$$\Delta y=L$$
$$v_x=\sin \theta \cdot v_i$$
$$x=\frac{2 \cdot L \cdot v_i \cdot \sin \theta}{\sqrt{v_f^2-v_x^2}+v_i \cdot \cos \theta}$$

Replacing vf with (1) and replacing vx:
Edit: I've made a mistake replacing vx^2

Spoiler: Mistake

$$x=\frac{2 \cdot L \cdot v_i \cdot \sin \theta}{\sqrt{v_i^2+\frac{2 \cdot F_e \cdot L}{m}-\sin^2 \theta \cdot v_f^2}+v_i \cdot \cos \theta}$$

$$x=\frac{2 \cdot L \cdot v_i \cdot \sin \theta}{\sqrt{v_i^2+\frac{2 \cdot F_e \cdot L}{m}-\sin^2 \theta \cdot \left(v_i^2+\frac{2 \cdot F_e \cdot L}{m} \right)}+v_i \cdot \cos \theta}$$
$$x=\frac{2 \cdot L \cdot v_i \cdot \sin \theta}{\sqrt{v_i^2+\frac{2 \cdot F_e \cdot L}{m}-\sin^2 \theta \cdot v_i^2 + \sin^2 \theta \cdot \frac{2 \cdot F_e \cdot L}{m}}+v_i \cdot \cos \theta}$$
$$x=\frac{2 \cdot L \cdot v_i \cdot \sin \theta}{\sqrt{v_i^2(1- \sin^2 \theta) +\frac{2 \cdot F_e \cdot L}{m}(1+\sin^2 \theta)}+ \cos \theta \cdot v_i}$$

$$x=\frac{2 \cdot L \cdot v_i \cdot \sin \theta}{\sqrt{v_i^2+\frac{2 \cdot F_e \cdot L}{m}-\sin^2 \theta \cdot v_i^2}+v_i \cdot \cos \theta}$$
$$x=\frac{2 \cdot L \cdot v_i \cdot \sin \theta}{\sqrt{v_i^2 \left( 1+ \frac{2 \cdot F_e \cdot L}{m \cdot v_i^2}-\sin^2 \theta \right) }+v_i \cdot \cos \theta}$$
$$x=\frac{2 \cdot L \cdot v_i \cdot \sin \theta}{v_i \sqrt{ 1+ \frac{2 \cdot F_e \cdot L}{m \cdot v_i^2}-\sin^2 \theta }+v_i \cdot \cos \theta}$$
$$x=\frac{2 \cdot L \cdot v_i \cdot \sin \theta}{v_i \left( \sqrt{ 1+ \frac{2 \cdot F_e \cdot L}{m \cdot v_i^2}-\sin^2 \theta }+ \cos \theta \right)}$$
$$x=\frac{2 \cdot L \cdot \sin \theta}{\sqrt{ 1+ \frac{2 \cdot F_e \cdot L}{m \cdot v_i^2}-\sin^2 \theta }+ \cos \theta}$$

Finally I know that:
$$V=\frac{U_e}{q}=\frac{F_e \cdot L}{q}$$
$$F_e \cdot L=V \cdot q$$

$$x=\frac{2 \cdot L \cdot \sin \theta}{ \sqrt{ 1+ \frac{2 \cdot V \cdot q}{m \cdot v_i^2}-\sin^2 \theta }+ \cos \theta}$$

Now I've an equation which gives me the position as function of voltage. Can I do $\frac{\partial x}{\partial V}$ in order to obtain how much the position varies in relation with small variation $\partial V$?

Am I doing it in a adequated way (I think that it's a really ugly equation)? Or should I consider other factors?

 

[Orodruin]

Your idea is correct. However, you have some errors in your derivation of $x(V)$. For example, you have used $v_x^2 = v_f^2 \sin^2\theta$ rather than $v_x^2 = v_i^2 \sin^2\theta$.

 

[RmsAdd]

Thank you very much @Orodruin !
I corrected it.
Then I've to do $\frac{\partial x}{\partial V}$.
$$x(V)=\frac{2 \cdot L \cdot \sin \theta}{ \sqrt{ 1+ \frac{2 \cdot V \cdot q}{m \cdot v_i^2}-\sin^2 \theta }+ \cos \theta}$$
$$\frac{\partial x}{\partial V} = \frac{ \frac{-2L \sin \theta \cdot \frac{2q}{m \cdot v_i^2} }{2 \sqrt{1+\frac{2Vq}{m \cdot v_i^2}-\sin^2 \theta}} }{ \left( \cos \theta + \sqrt{1+\frac{2Vq}{m \cdot v_i^2} - \sin^2 \theta } \right)^2 }$$
$$\frac{\partial x}{\partial V} = \frac{ -2Lq \sin \theta }{ m \cdot v_i^2 \left( \cos \theta + \sqrt{1+\frac{2Vq}{m \cdot v_i^2}-\sin^2 \theta } \right) ^2 \sqrt{ 1+\frac{2Vq}{m \cdot v_i^2}-\sin^2 \theta } }$$

Does that equation answers the question about "Where and how much the position where electrons impact varies" or should I find something else?

 

[haruspex]

cuatic effects

For your information, the English is "quantum effects".
I would have treated it like a gravitational trajectory question, using the SUVAT equations, but it's probably no simpler.
You could simplify your final expression a bit by collapsing 1-sin² to cos² and creating a name for the group $\frac{2q}{mv_i^2}$, which occurs in three places.