Like Tony Stark
- 182
- 6
- Homework Statement
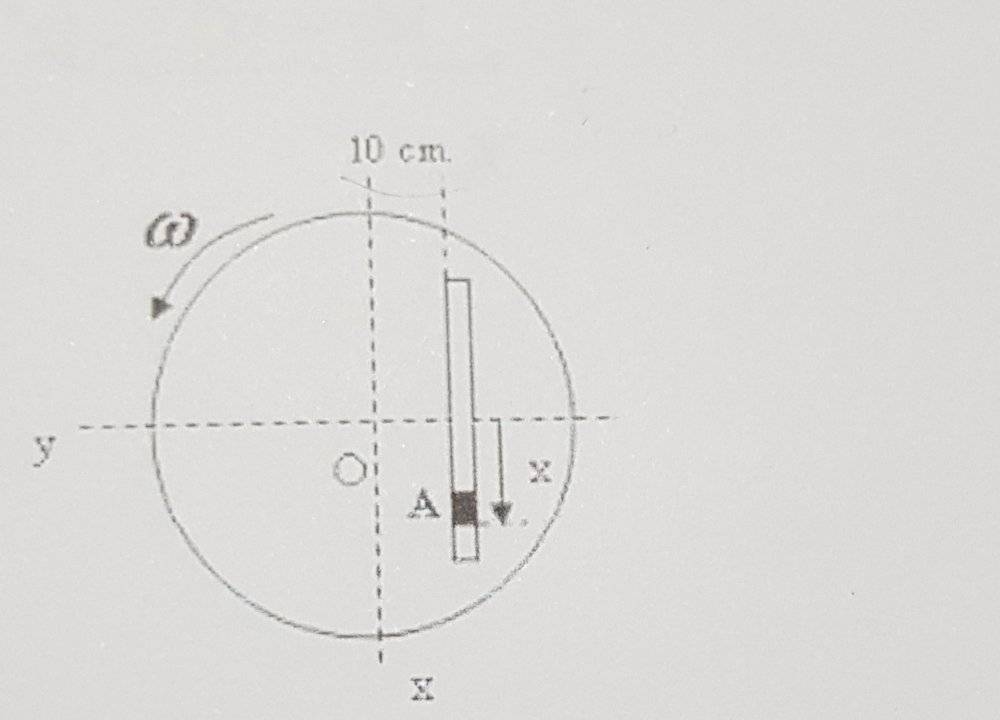
- The particle ##A## moves along the groove while the disc turns about ##O## with an angular velocity ##\omega##. Find the ##x## and ##y## components of the acceleration of ##A## with respect to Earth when ##\omega =3 rad/s ; \dot{\omega}=-10 rad/s^2 ; x=7.5 cm ; v_x =10 cm/s## and ##a_x =15 cm/s^2##.
- Relevant Equations
- ##\vec a=\vec a_B + \vec{\dot \omega} \times \vec r + \vec \omega \times (\vec \omega \times \vec r) + 2. (\vec \omega \times \vec v_{rel}) + \vec a_{rel}##
Well, I tried plugging the data in the formula. I know that ##\vec a_b = 0; \vec \omega=3 rad/s ; \vec r## can be calculated using trigonometry. Then I also know that ##v_{relx}= 10 cm/s##, ##a_{relx}=15 cm/s^2##, ##\vec {\dot{\omega}}=-10 rad/s^2##.
But how do I get ##v_{rely}## and ##a_{rely}##? And what's the difference between ##\vec a_{rel}## and ##\vec a##?
But how do I get ##v_{rely}## and ##a_{rely}##? And what's the difference between ##\vec a_{rel}## and ##\vec a##?