Particle waves through a potential barrier

[DivGradCurl]

Hi all,

I came across this figure in a textbook. Simple stuff, but can get tricky:

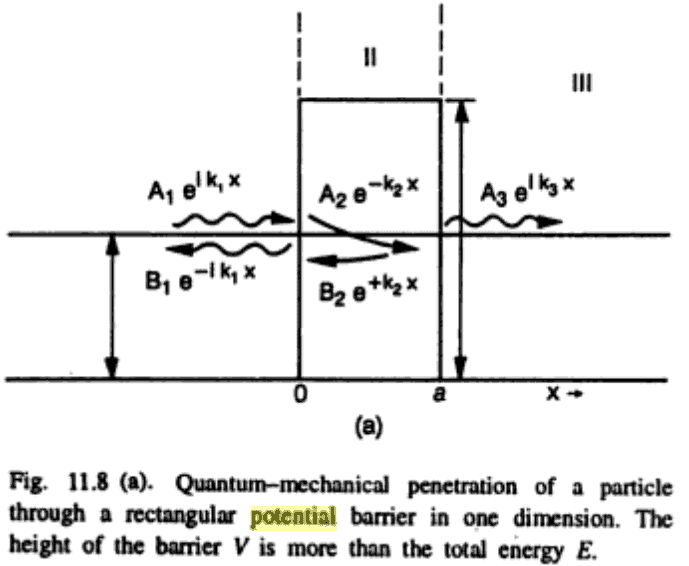
I don't understand why the sign convention flips upon entering the barrier (region II), but I guess the book is correct and that I should just take it as a fact.

If anybody has a reasonable thought to add so I'm making sense out of this rather than just accepting it, please let me know.

Thanks!

 

[blue_leaf77]

Physical intuition, a barrier is supposed to prevent a particle from passing through, therefore we must expect the probability to find the particle beyond the barrier is lower than it is before.

 

[cpsinkule]

What do you mean by sign convention? The solution to the Schrödinger equation for a particle in a region where the potential is larger than the energy is a sum of a decaying and growing exponentials.

 

[jtbell]

You're free to swap the signs on the exponents in the A₂ and B₂ terms when setting up the solution, but then the values of A₂ and B₂ will also get swapped when you actually work out the solution.

 

[DivGradCurl]

Hey thanks for the explanation, jtbell. That makes sense now.