matermultorum
- 7
- 0
1. I don’t have a diagram to add, but it is a simple system.
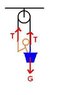
1 pulley at the top. On the left is a bucket with a person in it. On the right the rope hangs and the person(in the bucket) is pulling down on the rope with unknown force. The system is moving at constant velocity.
Problem: A person pulls himself up using a bucket and pulley apparatus. How hard must he pull downward on the right to lift himself and the bucket on the left? Mass of bucket/person is 65kg.
2. 2T=mg 2T=65(9.8) T=318.5N
3. Intuitively and from the answer key,I know the answer. I know that the up and down forces are equal because the acceleration is zero. What I don’t know how to draw the free body diagram or how to explain it. There is only one free body diagram, correct? That of the bucket/person?
What are the forces acting on the bucket/person? Here are the two options that get the right answer. Does either one shows correct thinking (I won’t be surprised to find that neither do). Can you help me get the explanations corrected?
FIRST TRY-Forces acting on the bucket/person
Up :Tension in rope T
Down: mg-T directed down because when the person pulls it lessens their weight by the amount of the pull
SECOND TRY-Forces acting on the bucket/person
Up: twice the tension in the rope because there is one pulley and the force going down from the pulley also acts up on the rope on the bucket side
Down: mg
Thank you,
matermultorum
1 pulley at the top. On the left is a bucket with a person in it. On the right the rope hangs and the person(in the bucket) is pulling down on the rope with unknown force. The system is moving at constant velocity.
Problem: A person pulls himself up using a bucket and pulley apparatus. How hard must he pull downward on the right to lift himself and the bucket on the left? Mass of bucket/person is 65kg.
2. 2T=mg 2T=65(9.8) T=318.5N
3. Intuitively and from the answer key,I know the answer. I know that the up and down forces are equal because the acceleration is zero. What I don’t know how to draw the free body diagram or how to explain it. There is only one free body diagram, correct? That of the bucket/person?
What are the forces acting on the bucket/person? Here are the two options that get the right answer. Does either one shows correct thinking (I won’t be surprised to find that neither do). Can you help me get the explanations corrected?
FIRST TRY-Forces acting on the bucket/person
Up :Tension in rope T
Down: mg-T directed down because when the person pulls it lessens their weight by the amount of the pull
SECOND TRY-Forces acting on the bucket/person
Up: twice the tension in the rope because there is one pulley and the force going down from the pulley also acts up on the rope on the bucket side
Down: mg
Thank you,
matermultorum
Last edited: