Photoelectric effect and work function

[stickplot]

Homework Statement

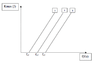
a. Which plot on the graph represents the metal with the lowest work function?

b. What does the slope of the graphs represent? (graph is attached)

Homework Equations

threshold frequency= work function/ planks constant

The Attempt at a Solution

a. the lower the work function, the lower the frequency, so (im still confused about the graph)
so plot 1 is the one with the lowest work function.
b. the slope on the graph shows the amount of energy frequency that it took for a photoelectric effect to occur.

im not to sure about my answers someone help out please.

 

[Kurdt]

I can't see the graph but if its kinetic energy versus frequancy then there will be a straight line relationship.

$$T = h\nu -\phi$$

Compare that with the equation of a straight line $y=mx+c$.

 

[stickplot]

o ok i got it
i understand the graph now. it is a kinetic energy vs frequency graph.

a. the plot with the lowest work function is 1, because it supports the least amount of frequency. The one that supports the least amount is the one that causes a photoelectric effect first
b. the three slopes are equal to Planck's Constant which shows that the energy to frequency relation is constant for all materials. It also shows the difference between each one and compare how much threshold frequency they each support.

how is that?

 

[Kurdt]

Looks good. For b all you need say is it represents Planck's constant.

 

[stickplot]

alright thank you

 

[rahmatkat]

Explain why the backing volts depends on the frequency of light but not on the intensity.