Bashyboy
- 1,419
- 5
Homework Statement
A certain quaternary star system consists of three stars, each of mass m, moving in the same circular orbit of radius r about a central star of mass M. The stars orbit in the same sense and are positioned one-third of a revolution apart from one another. Show that the period of each of the three stars is given by
Homework Equations
The Attempt at a Solution
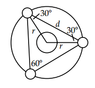
What I am having difficulty is with the geometry of this problem. I attached a diagram that the answer key provides. How am I to know that the three planets form a equilateral triangle, what betokens this. Likewise, why is the angle between two sides of the triangle 60 degrees?
 … you should be able to prove this in about 17 different ways!
… you should be able to prove this in about 17 different ways!