Planar Kinetics of a Rigid Body

[jjiimmyy101]

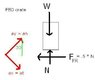
QUESTION: The 50 kg uniform crate rests on the platform for which the coefficient of static friction is us = 0.5. If the supporting links have an angular velocity w = 1 rad/s, determine the greatest angular acceleration they can have so that the crate does not slip or tip at the instant theta = 30 as shown in the attachment.

I have no clue where to even begin.

I need a hint or hints to start the problem. Please...anyone.

 

[Soveraign]

Ew. Well, start thinking about converting your angular acceleration to what that means in the x and y directions when the angle is 30 degrees. Keep in mind with regard to friction that 1) the y-acceleration will affect the normal force of the crate, thus affecting the frictional force and 2) the x-acceleration can be used to figure what lateral force the beam is creating on the crate, and since they mentioned it, 3) how the existing angular velocity affects the x and y accelerations on that beam due to the circular motion. When you have all the contributions to x and y acceleration, they can simply be added in the x and y directions independently so you should be able to get some good relations from the individual parts.

So, with regard to the "tipping over" part, similarly to above, you need to consider how the x and y accelerations contribute to the stability of this crate. I suppose were I to do this problem, I would start out by treating the two situations separately and then looking at which angular acceleration is smaller for the final answer.

Man, this sounds like an evil engineering dynamics problem.

 

[jjiimmyy101]

ax = at = (angular acceleration) * radius

ay = an = (angular velocity) * radius

radius = 4


Am I getting there? How's my FBD of the crate look?

 

[Soveraign]

The accelerations due to 1) the angular velocity and 2) the angular acceleration can each be broken down into x and y components.

Looking at the angular velocity case, you know that there is a centripetal acceleration in the direction parallel to the supporting links. This follows the familiar a = v^2/r where v = \omega r. Thus, a_x = a \cos(\theta) and a_y = a\sin(\theta) where \theta is the angle measured from the horizontal (i.e. 60 degrees).

So, putting these together you get the x and y contributions to acceleration due to the angular velocity as:

a_x = \omega^2 r \cos(\theta) and a_y = \omega^2 r \sin(\theta).

Now, the contributions from angular acceleration would be due to a traditional acceleration vector in the direction perpendicular to the supporting links with magnitude a = \alpha r. You can break down the x and y components after thinking about what direction this vector points.


At this point I'd like to stress that I may not be solving this in a way that your instructor intends. The overall idea is to find the total of the x and y accelerations on the box and then see how this affects the forces. For example, the normal force N would be the mass of the box times the sum of the accelerations due to gravity, angular velocity, and angular acceleration (keeping in mind some of these are negative). Also, it has been a while since I've had mechanics so I might be missing an easier way to do this.

 

[jjiimmyy101]

angular acceleration:

ax = \alpha r cos30
ay = \alpha r sin30

Then:

ax(total) = \sqrt(2^2 + (3.4641 \alpha)^2)
ay(total) = \sqrt(3.4641^2 + (-2 \alpha)^2)


So then I should solve these equations:

\sum Fx = max = -0.5*N = 50 *(\sqrt(4 + 12 \alpha^2)
\sum Fy = may = -W + N = 50 *(\sqrt(12 + 4 \alpha^2)

Am I doing it right? I don't want to go any further if I'm wrong because those look like two tough equations to solve (very tedious). Thanks.

 

[Soveraign]

Looks like you have the right idea for angular acceleration, although the vector is 30 degrees below the horizontal, so that would be a negative 30 degrees.

This would make the total accelerations:

a_{xf} = \alpha r \cos(-30) + \omega^2 r \cos(30)
a_{yf} = g + \alpha r \sin(-30) + \omega^2 r \sin(30)

(where g = -9.8, note y acceleration due to angular velocity is opposite direction to the other two and I have chosen down to be negative)

and thus, for example, the normal force N = m a_{yf} leads to a frictional force of
F_{fric} = \mu m a_{yf} = \mu m (g + \alpha r \sin(-30) + \omega^2 r \sin(30))

The lateral force applied to this mass then becomes
F_{lat} = m a_{xf} = m (\alpha r \cos(-30) + \omega^2 r \cos(30))

so to figure out the maximum angular acceleration you can apply before the crate slides, set F_{fric} = F_{lat} and solve for \alpha (I think ).

 

[jjiimmyy101]

Thanks and sorry for not responding sooner.

\alpha = -1.651 is the answer I get when I solve F_{fric} = F_{lat}
but the answer is supposedly \alpha = 0.587


I was just wondering if you're taking into consideration if it tips at this instant as well as slips. I don't know what's going on and I sure wouldn't have gotten this far without you, so I'm just throwing out suggestions now. I'm at the brink of just giving up on this question...it's starting to annoy me.