progiangbk
- 13
- 0
Hi there,
My teacher gave me a homework, but this Theory of Plasticity is new and difficult to me.
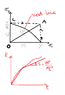
He has calculated the strain according to path (1), now I have to do with the path (2) and (3).
This is what he did with path (1):
ε11=∫(1/E)dσ11 + ∫[(σ11/S)(σ11dσ11+3σ12dσ12)]/(σ11^2 + 3σ12^2)
the first and second terminals for the above integration are (0,Y) and (0,Y/√3)
Finally he got:
ε11= (Y/E) + (Y/S)ln√2
Please help me with path (2) or pah (3) or both, or tell me how to solve it.
Thanks and best regards
My teacher gave me a homework, but this Theory of Plasticity is new and difficult to me.
He has calculated the strain according to path (1), now I have to do with the path (2) and (3).
This is what he did with path (1):
ε11=∫(1/E)dσ11 + ∫[(σ11/S)(σ11dσ11+3σ12dσ12)]/(σ11^2 + 3σ12^2)
the first and second terminals for the above integration are (0,Y) and (0,Y/√3)
Finally he got:
ε11= (Y/E) + (Y/S)ln√2
Please help me with path (2) or pah (3) or both, or tell me how to solve it.
Thanks and best regards