Plotting a wavefunction for a finite potential well doesn't work out

[71GA]

Lets say we have a finite square potential well like below:

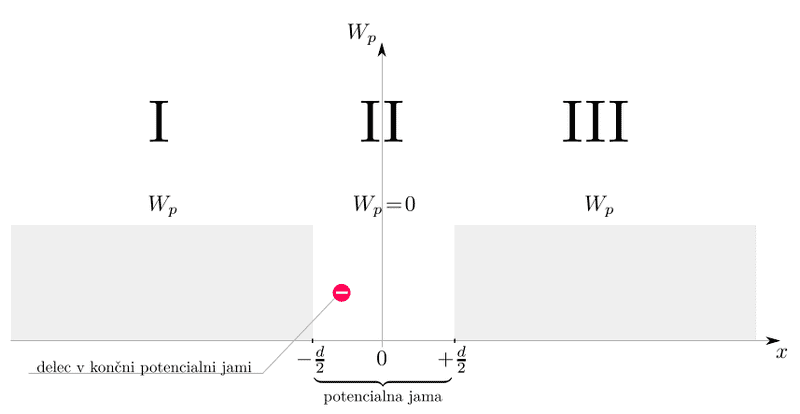
This well has a $\psi$ which we can combine with $\psi_I$, $\psi_{II}$ and $\psi_{III}$. I have been playing around and got expressions for them, but they are not the same for ODD and EVEN solutions but let's do this only for ODD ones.

ODD solutions:

$$
\boxed{\psi_{I}= Ae^{\mathcal{K} x}~~~~~~~~\psi_{II}= - \dfrac{A e^{-\mathcal{K}\tfrac{d}{2}}}{\sin\left( \mathcal{L} \tfrac{d}{2} \right)}\, \sin\left(\mathcal{L} x\right)~~~~~~~~
\psi_{III}=-Ae^{-\mathcal{K} x}}
$$

When i applied boundary conditions to these equations i got transcendental equation which is:

\begin{align}
&\boxed{-\dfrac{\mathcal{L}}{\mathcal{K}} = \tan \left(\mathcal{L \dfrac{d}{2}}\right)} && \mathcal L \equiv \sqrt{\tfrac{2mW}{\hbar^2}} && \mathcal K \equiv \sqrt{\tfrac{2m(W_p-W)}{\hbar^2}} \\
&{\scriptsize\text{transcendental eq.} }\\
&\boxed{-\sqrt{\tfrac{1}{W_p/W-1}} = \tan\left(\tfrac{\sqrt{2mW}}{\hbar} \tfrac{d}{2} \right)}\\
&{\scriptsize\text{transcendental eq. - used to graph} }
\end{align}

Transcendental equation can be solved graphically by separately plotting LHS and RHS and checking where crosssections are. $x$ coordinates of crossections represent possible (obviously quantized) energies $W$ in finite potential well. So i can theoreticaly get values for possible energies $W$ and when i get these i can calculate $\mathcal L$ and $\mathcal K$. I won't get constant $A$ which i can set as i like as it is not relevant. I decided to plot graphs for a speciffic case of an electron with mass $m_e$ which i put in a finite well. So the constants i know are:

\begin{align}
d &= 0.5nm\\
m_e &= 9.109\cdot 10^{-31} kg\\
W_p &= 25eV\\
\hbar &= 1.055 \cdot 10^{-34} Js {\scriptsize~\dots\text{well known constant}}\\
1eV &= 1.602 \cdot 10^{-19} J {\scriptsize~\dots\text{need this to convert from eV to J}}
\end{align}

I first used constants above to again draw a graph of transcendental equation and i found 2 possible energies $W$ (those aren't quite accurateas they are obtained graphically). The graph is very simmilar to graphs from other QM books:

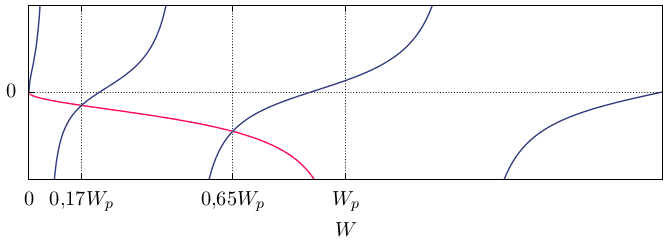
Lets chose only one of the possible energies and try to plot $\psi_I$, $\psi_{II}$ and $\psi_{III}$ for that same energy. I choose energy which is equal to $0.17\, W_p$ and calculate constants $\mathcal K$ and $\mathcal L$:

\begin{align}
\mathcal K &= 2.3325888\cdot 10^{10}\\
\mathcal L &= 1.5573994\cdot 10^{10}\\
\end{align}

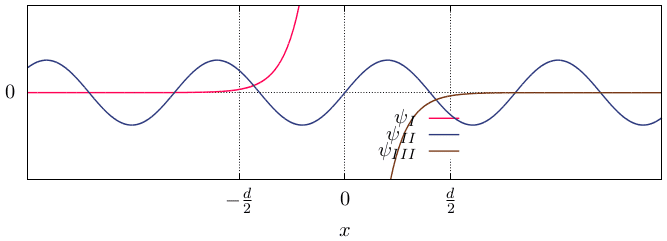
If i use those to plot $\psi_I$, $\psi_{II}$ and $\psi_{III}$, i notice that my boundary conditions at $-\tfrac{d}{2}$ and $\tfrac{d}{2}$ are not met:

QUESTION:
I did calculate my constants quite accurately, but i really can't read the energies (which are graphicall solutions to the first graph) very accurately. Does anyone have any suggestions on how to meet the boundary conditions? What's my problem here?

GNUPLOT script used to draw 2nd graph:

    set terminal epslatex color colortext size 9cm,5cm
    set size 1.5,1.0
    set output "potencialna_jama_6.tex"
    
    set style line 1 linetype 1 linewidth 3 linecolor rgb "#FF0055"
    set style line 2 linetype 2 linewidth 1 linecolor rgb "#FF0055"
    set style line 3 linetype 1 linewidth 3 linecolor rgb "#2C397D"
    set style line 4 linetype 2 linewidth 1 linecolor rgb "#2C397D"
    set style line 5 linetype 1 linewidth 3 linecolor rgb "#793715"
    set style line 6 linetype 2 linewidth 1 linecolor rgb "#793715"
    set style line 7 linetype 1 linewidth 3 linecolor rgb "#b1b1b1"
    set style line 8 linetype 3 linewidth 1 linecolor rgb "#b1b1b1"
    
    set grid
    
    set samples 7000
    
    set key at graph .70, 0.4
    set key samplen 2
    set key spacing 0.8
    
    m = 9.9109*10**(-31)
    d = 0.5*10**(-9)
    U = 25 * 1.602*10**(-19)
    h = 1.055*10**(-34)
    
    K = 2.3325888*10**10
    L = 1.5573994*10**10
    A = 1
    
    f(x) = A*exp(K*x)
    g(x) = -( A*exp(-L*(d/2)) )/( sin(L*(d/2)) )*sin(L*x)
    h(x) = -A*exp(-K*x)
    
    set xrange [-d:d]
    set yrange [-8*10**(-2):8*10**(-2)]
    
    set xtics ("$0$" 0, "$\\frac{d}{2}$" (d/2), "$-\\frac{d}{2}$" -(d/2))
    set ytics ("$0$" 0)

    set xlabel "$x$"
    
    plot [-1.5*d:1.5*d] f(x) ls 1 title "$\\psi_{I}$", g(x) ls 3 title "$\\psi_{II}$", h(x) ls 5 title "$\\psi_{III}$"

 

[mfb]

g(x) = -( A*exp(-L*(d/2)) )/( sin(L*(d/2)) )*sin(L*x)

The first L should be a K.

I think it's just a drawing problem. The functions have to meet at the edges of the potential well by construction.

 

[71GA]

The first L should be a K.

I think it's just a drawing problem. The functions have to meet at the edges of the potential well by construction.

This was the case thank you! After this my graphs still came out a bit weird but then i figured out that my graphical readings for energies was sloppy. Once i redid all the readings and recalculated $\mathcal L$ and $\mathcal K$ my graphs came out perfectly!