J89
- 29
- 0
Homework Statement
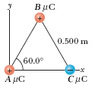
Three point charges are located at the corners of an equilateral triangle as in the figure below. Find the magnitude and direction of the net electric force on the 0.40 µC charge. (A = 0.20 µC, B = 6.60 µC, and C = -3.80 µC.). Diagram below...
Homework Equations
F= Ke |q1||q2|/r^2, cos and sin symbols
The Attempt at a Solution
a) .20*10^-6*(6.60*10^-6)*8.99*10^9/(.500)^2 = .0474672
b) .20*10^-6*(3.80*10^-6)*8.99*10^9/(.500)^2 =.0273296
.0474672*cos(240) = .015463926386
.0474672*sin(240) = .044877634258
= .015463926386 + .0273296 = .042793526386
.042793526386^2 + .044877634258^2 = .003845287957 = sqrt(.003845287957 ) = 0.062 N. Direction is 275 degrees. However, according the real solution, the answer is not 0.062! Can someone find what I did wrong here?