Polar coordinates and kinematics

[Telemachus]

Homework Statement

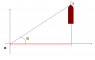
I've got some trouble and doubts with polar coordinates. I have this exercise, with a rocket going upwards, with a given acceleration. So I need to find the polar equation for the given situation for the position, the velocity and the acceleration. How should I proceed? I mean, I know I must find an equation that describes the path for r(t) in the polar form, but I'm not sure on how the acceleration fit on this.

The distance between the origin and the rocket "D" is given by the problem data.

Homework Equations

$$r(t)=r\vec{e_r}$$
$$v(t)=\dot r\vec{e_r}+r\dot \theta\vec{e_{\theta}}$$
$$a(t)=(\ddot r-r\dot \theta^2)\vec{e_r}+(r\ddot \theta+2 \dot r \dot \theta)\vec{e_{\theta}}$$

I think that $$r(t)$$ could be: $$r(t)=\sec \theta \vec{e_r}$$, but then I don't know how to work with the acceleration on the radial direction, or over the angle direction neither. Should I use trigonometry for this?

 

[Telemachus]

I've tried this way, but it doesn't looks fine really

$$a=k$$, $$s=kt$$ $$x=\displaystyle\frac{k}{2}t^2$$

Then the radial speed:
$$\dot r=s \cos \theta=kt \cos \theta$$

And the angular speed:
$$\dot \theta=s \sin \theta=kt \sin \theta$$

I think that the equation for r(t) should be $$\vec{r(t)}=\sec \theta \hat{e_r}$$. But I don't know how to work with it.

$$\dot r=v(t)=\dot r\vec{e_r}+r\dot \theta\vec{e_{\theta}}$$
$$\dot r=\sec r \tan r\hat{e_r}+\sec r \dot \theta \hat{e_{\theta}}$$

I don't know how to determine the radial speed and the angular speed, considering the acceleration, and I think what I've done doesn't make any sense.

Any help please?
Bye there.