Potential difference and static charge

[i0n]

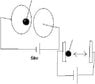
Hi I am doing a report on electrostatic force. It involves 2 steel plates which are connected to a 5kV DC power supply and are separated 8cm from each other. A table tennis ball painted in metallic paint (to conduct) is hung from a nylon wire between the two plates. When the power supply is switched on and the ball makes contact with one of the plates it begins oscillating, i.e. bouncing from one plate to the other and back again acting as a charge carrier. See my brilliantly drawn diagram :tongue:

I am wondering why such a high voltage is required to get the ball oscillating, i.e. if i turn the powersupply down to 2kV the electrostatic force is not strong enough to "pull" the ball toward the oppositely charged plate and it stops in the middle. Any ideas would be helpfull along with relevant equations.

P.S. I've measured the current and it is very small (10-100 nano amps)

 

[Nate810]

The reason that you need a high voltage in order to get the ball oscillating is because of the nature of electrostatic force. The electrostatic force between two charged objects is proportional to the product of their charges and inversely proportional to the square of the distance between them. This means that in order for the force to be strong enough to pull the ball towards the oppositely charged plate, the voltage would need to be high enough to create a large enough charge on each plate. Mathematically, this can be expressed as follows: F = k * (Q1 * Q2)/r^2Where F is the electrostatic force, k is Coulomb's constant (8.99 x 10^9 N m^2/C^2), Q1 and Q2 are the charges of the two plates, and r is the distance between them. So, if you decrease the voltage, the charge on each plate will be smaller, which means the electrostatic force will be weaker and not be able to pull the ball towards the oppositely charged plate.

 

[wais]

Hi there,

Thank you for sharing your experiment and question with us. It's great to see that you're exploring the concept of electrostatic force and potential difference.

To understand why a high voltage is required to get the ball oscillating, we need to first understand the concept of potential difference. Potential difference, also known as voltage, is the difference in electrical potential between two points. In your experiment, the 5kV DC power supply creates a potential difference between the two steel plates. This means that one plate has a higher electrical potential than the other, and this difference in potential creates an electric field between the plates.

Now, when the metallic ball is suspended between the plates, it experiences a force due to the electric field. This force is known as the electrostatic force, and it is directly proportional to the electric field strength and the charge of the object. In your experiment, the ball is acting as a charge carrier, meaning it has a net charge due to the metallic paint. When the power supply is turned on, the ball experiences a strong electrostatic force due to the high voltage, causing it to oscillate between the plates.

When you reduce the voltage to 2kV, the potential difference between the plates is not strong enough to produce a significant electric field. This means that the electrostatic force acting on the ball is weaker, and it is not enough to overcome the ball's inertia and make it oscillate. This is why the ball stops in the middle.

To better understand the relationship between voltage, electric field, and electrostatic force, you can use the equation F = qE, where F is the electrostatic force, q is the charge of the object, and E is the electric field strength.

I hope this helps to answer your question. Keep up the great work with your experiment and don't hesitate to ask if you have any further questions. Happy experimenting!