Power dissapatied by a resistor

  • Thread starter Thread starter talaroue
  • Start date Start date
  • Tags Tags
    Power Resistor
AI Thread Summary
The discussion centers on calculating the power dissipated by a resistor (R1) in a circuit with two resistors in series. The user initially applies the formula for equivalent resistance in parallel instead of series, leading to confusion in their calculations. They correctly identify the current using I=V/R but mistakenly apply the wrong resistance formula. The conversation highlights the importance of using the correct formulas for series and parallel circuits to accurately determine power dissipation. Clarification is needed on the correct approach to solve the problem.
talaroue
Messages
302
Reaction score
0

Homework Statement



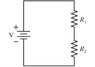
How much power is dissipated by R1 resistor? (R1=15 W, R2=25 W, V=9 V.)

Resistor.jpg


Homework Equations



I=V/R

P=I^2R

The Attempt at a Solution


Since it is a series 1/Req=(1/R1)+(1/R2)

Then I=V/R= .96 A

so Then i just simply plugged in I in P=I^2R which is apparently wrong, but I thought this is right. What am i doing wrong?
 

Attachments

  • Resistor.jpg
    Resistor.jpg
    12.7 KB · Views: 360
Physics news on Phys.org
You are right, the resistors are in series. So why are you using the Req formula for resistors in parallel?
 
...let me get back to you
 

Thread 'Errors and significant figures'

I multiplied the values first without the error limit. Got 19.38. rounded it off to 2 significant figures since the given data has 2 significant figures. So = 19. For error I used the above formula. It comes out about 1.48. Now my question is. Should I write the answer as 19±1.5 (rounding 1.48 to 2 significant figures) OR should I write it as 19±1. So in short, should the error have same number of significant figures as the mean value or should it have the same number of decimal places as...
View full post »
Thread 'A cylinder connected to a hanging mass'

Thread 'A cylinder connected to a hanging mass'

Let's declare that for the cylinder, mass = M = 10 kg Radius = R = 4 m For the wall and the floor, Friction coeff = ##\mu## = 0.5 For the hanging mass, mass = m = 11 kg First, we divide the force according to their respective plane (x and y thing, correct me if I'm wrong) and according to which, cylinder or the hanging mass, they're working on. Force on the hanging mass $$mg - T = ma$$ Force(Cylinder) on y $$N_f + f_w - Mg = 0$$ Force(Cylinder) on x $$T + f_f - N_w = Ma$$ There's also...
View full post »

Similar threads

Batteries in series, parallel, and internal resistance
Replies
24
Views
5K
Why is it important to classify circuits as series or parallel?
Replies
5
Views
2K
Finding the Current in a Resistor in a Closed Circuit
Replies
4
Views
2K
Power formula for circuit when another resistor is added in
Replies
9
Views
2K
Electromagnetism problem: Merging of 2 charged drops of mercury
Replies
2
Views
1K
What Power Is Dissipated by the R2 Resistor?
Replies
5
Views
7K
How to calculate R1 and R2 in this RC circuit
Replies
3
Views
3K
Total equivalent resistance of a combined circuit
Replies
7
Views
2K
Power dissipated in this circuit with 2 batteries and 3 resistors
Replies
22
Views
4K
High voltage circuit with voltmeter in between
Replies
3
Views
2K

Hot Threads

Recent Insights

Back
Top