Mosaness
- 92
- 0
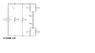
1. Making appropriate use of resistor combination techniques, calculate i3 in the circuit of Fig. 3.84 and the power provided to the circuit by the single current source.
2. Connected in Parallel and Series. Ohm's Law. KCL/KVL
3. I honestly am just guessing how to do this one:
The 3 ohms and 5 ohms resistors are in parallel to one another, so combining their resistance should give 1.875 ohms. The 3 ohms and the 9 ohms resistors too are in parallel, so they should give a total resistance of 2.25 ohms, which can be added to the 3 ohms and 5 ohms in the rightmost branch, to give 10.25 ohms. That leaves us with another pair of resistors in parallel, the 3 ohms and the 6 ohms, which when combined give us 2 ohms.
Now we have two resistors in parallel. The resistor of 1.875 ohms and the resistor of 12.25 ohms. This gives a total resistance of 1.626 ohms.
This can be used to find what I3 is:
1 - 1.626(I3) = 0
I3 = 0.615 A
Now that we know what I3 is, we can calculate the power source using the current.
2. Connected in Parallel and Series. Ohm's Law. KCL/KVL
3. I honestly am just guessing how to do this one:
The 3 ohms and 5 ohms resistors are in parallel to one another, so combining their resistance should give 1.875 ohms. The 3 ohms and the 9 ohms resistors too are in parallel, so they should give a total resistance of 2.25 ohms, which can be added to the 3 ohms and 5 ohms in the rightmost branch, to give 10.25 ohms. That leaves us with another pair of resistors in parallel, the 3 ohms and the 6 ohms, which when combined give us 2 ohms.
Now we have two resistors in parallel. The resistor of 1.875 ohms and the resistor of 12.25 ohms. This gives a total resistance of 1.626 ohms.
This can be used to find what I3 is:
1 - 1.626(I3) = 0
I3 = 0.615 A
Now that we know what I3 is, we can calculate the power source using the current.