- #1
barbarahowser
- 3
- 0
Hi,
I am trying to analyze a composite part which is made of carbon/epoxy and has [+45/-45]2s as the layup. I got the following material properties for carbon/epoxy from the textbook "Engineering Mechanics of Composite Materials", by I.M. Daniel & O. Ishai,
Longitudinal Modulus, E1=147Gpa
Transverse In-plane, E2=10.3Gpa
Transverse out of plane, E3=10.3Gpa
In plane shear modulus, G12=7Gpa
Out of plane shear modulus, G23=3.7Gpa
Out of plane shear modulus, G13=7Gpa
Major in-plane Poisson's ratio, niu12=0.27
Major in-plane Poisson's ratio, niu23=0.54
Major in-plane Poisson's ratio, niu13=0.27
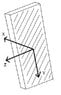
The coordinate system of the part is shown in figure attached with the fiber laid up in the YZ plane. Can someone please tell me how I can transform the material properties given above into the coordinate system shown in (composite part.jpeg)
Thanks,
Barbara
I am trying to analyze a composite part which is made of carbon/epoxy and has [+45/-45]2s as the layup. I got the following material properties for carbon/epoxy from the textbook "Engineering Mechanics of Composite Materials", by I.M. Daniel & O. Ishai,
Longitudinal Modulus, E1=147Gpa
Transverse In-plane, E2=10.3Gpa
Transverse out of plane, E3=10.3Gpa
In plane shear modulus, G12=7Gpa
Out of plane shear modulus, G23=3.7Gpa
Out of plane shear modulus, G13=7Gpa
Major in-plane Poisson's ratio, niu12=0.27
Major in-plane Poisson's ratio, niu23=0.54
Major in-plane Poisson's ratio, niu13=0.27
The coordinate system of the part is shown in figure attached with the fiber laid up in the YZ plane. Can someone please tell me how I can transform the material properties given above into the coordinate system shown in (composite part.jpeg)
Thanks,
Barbara