zartiox
- 2
- 0
Hi guys.
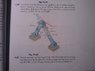
Please look at the uploaded picture.
Normal stress is difined as: σ= P/A. And the Maximum normal stress σ = P/ (b*h/cos(θ)) ??
The right answers should be σAB= 97,7 MPa and σBC = -66,5 MPa. But how do I calculate it?
What I have tried:
Force AB: 40* sin(60deg) = 34,641 kN = 34,641 * 10^3 N
σAB= 34,641 * 10^3 N/((45-20)*12)/sin(60deg)) = 100 MPa
Please look at the uploaded picture.
Normal stress is difined as: σ= P/A. And the Maximum normal stress σ = P/ (b*h/cos(θ)) ??
The right answers should be σAB= 97,7 MPa and σBC = -66,5 MPa. But how do I calculate it?
What I have tried:
Force AB: 40* sin(60deg) = 34,641 kN = 34,641 * 10^3 N
σAB= 34,641 * 10^3 N/((45-20)*12)/sin(60deg)) = 100 MPa