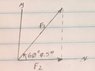Problem with Approximations Using Differentials

[rhdinah]

Homework Statement

I am working on this problem and having difficulty getting the required answer. It is the exact problem as here , but I’m still not getting it.

BTW this is problem 10, Section 4, Chapter 4 Partial Differentiation from M. Boas’s book Mathematical Methods in the Physical Sciences, 3rd edition.

A force 500 nt is measured with a possible error of 1 nt. Its component in a direction 60° away from its line of action is required, where the angle is subject to an error of 0.5°. What is (approximately) the largest possible error in the component?

Homework Equations

The Attempt at a Solution

We are going to use differentials here.

$Component = F_1*sin(\theta)$

$\frac{d Component}{Component} = \frac {d F_1}{F_1} + \frac {d sin(\theta)}{sin(\theta)} d \theta$

$\frac{d Component}{Component} = \frac {d F_1}{F_1} + \frac {cos(\theta)}{sin(\theta)} d \theta$

$Largest \left|\frac{d Component}{Component}\right| = \left|\frac {d F_1}{F_1}\right| + \left|\frac {cos(\theta)}{sin(\theta)} d \theta\right| = \frac{1}{500}+\frac{cos(\frac{\pi}{3})}{sin(\frac{\pi}{3})} * \frac{0.5}{60} = .002 + cot(\frac{\pi}{3}) * \frac{0.5}{60} = .002 + 0.00481 = 0.00681$

So the $Component = 500 sin(\frac{\pi}{3}) = 433$

$Component Error = 433*0.00681 = 2.95$ … which is not the correct answer of 4.28 nt

So if someone can direct me to my error I'd certainly appreciate it! Thank you!

 

[Orodruin]

You have used $d\theta/\theta$ instead of $d\theta$ in your computation. Note that you also need to put it in radians based on how you treated the derivative.

 

[rhdinah]

Thank you Orodruin! Let me put your ideas in motion!

$Largest \left|\frac{d Component}{Component}\right| = \left|\frac {d F_1}{F_1}\right| + \left|\frac {cos(\theta)}{sin(\theta)} d \theta\right| = \frac{1}{500}+\frac{cos(\frac{\pi}{3})}{sin(\frac{\pi}{3})} * \frac{0.5\pi}{180} = .002 + cot(\frac{\pi}{3}) * \frac{0.5\pi}{180} = .002 + 0.00504 = 0.00704$

So the $Component = 500 sin(\frac{\pi}{3}) = 433$

$Component Error = 433*0.00704 = 3.05$ … which is still not the correct answer of 4.28 nt

So I suspect there's something seriously wrong with my approach ... my equation ... any further ideas that could lead me to a correct solution please? :-) Thank you!

 

[Orodruin]

What is the component of a force in a direction to which it makes an angle $\theta$?

 

[rhdinah]

Yes, thank you so much! I looked at my original diagram and realized that I had the trig wrong! Shame on me! I was mislead a bit by the ref thread. I should have trusted my original diagram and not listened to the banter on that thread.

To correct this:
$Largest \left|\frac{d Component}{Component}\right| = \left|\frac {d F_1}{F_1}\right| + \left|\frac {sin(\theta)}{cos(\theta)} d \theta\right| = \frac{1}{500}+\frac{sin(\frac{\pi}{3})}{cos(\frac{\pi}{3})} * \frac{0.5\pi}{180} = .002 + tan(\frac{\pi}{3}) * \frac{0.5\pi}{180} = .002 + 0.0151 = 0.0171$

So the $Component = 500 nt\hspace{.1cm} cos(\frac{\pi}{3}) = 250 nt$

$Component Error = 250 nt*0.0171 = 4.28 nt$ … which is the correct answer.$\hspace{1cm}\square$