bibo_dvd
- 37
- 0
hello guys :)
i need your help with this problem
i can understand that in (a) we will use the integral of row(v) * dv to get the charge
and in (b) we will use the formule D(r)=Q/[4*PI*r^2]
but in (C) should it be zero or what ??
and if it should be zero why in the solution manual it uses the formula of D(r)=Q[4*PI*(r^2)] again ?!
i don't know what is the right answer for this ..so i need your help ..Thanks guys :)

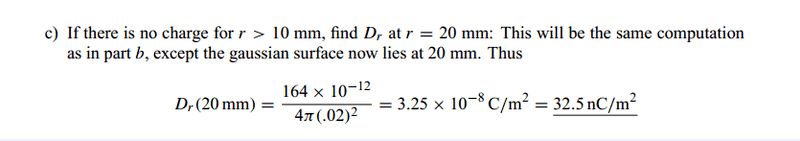
i need your help with this problem
i can understand that in (a) we will use the integral of row(v) * dv to get the charge
and in (b) we will use the formule D(r)=Q/[4*PI*r^2]
but in (C) should it be zero or what ??
and if it should be zero why in the solution manual it uses the formula of D(r)=Q[4*PI*(r^2)] again ?!
i don't know what is the right answer for this ..so i need your help ..Thanks guys :)