Problem with making the correct FBD

[Better WOrld]

Homework Statement

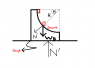
Consider a wedge of mass $m$ whose upper surface is a quarter circle and is smooth. The lower part is rough. A small block of same mass is kept at the topmost position and the initial position is shown in figure. The block slides down the wedge.

Find the minimum value of coefficient of friction between floor and lower surface of wedge so that the wedge remains stationery during the block's motion on it.

Homework Equations

The Attempt at a Solution

I managed to calculate the normal force $N$ exerted by the wedge on the block. This comes out to be $3mg\sin\theta$. This is also the force exerted by the block on the wedge. However, when I tried to find the normal reaction of the ground on the wedge, Iran into problems.

According to me, we should include the weight of the wedge ($W_W$)+ the vertical component of $N$ + the weight of the block ($W_B$ and equate all of them with $N'$ (the normal force acting on the wedge). In other words, $$N'=W_W +N\sin\theta+W_B$$

However, the solution given equates the normal reaction on the wedge by $$N'=W_W+N\sin\theta$$

Could somebody please explain why we ignore the force exerted on the wedge by the block while calculating the normal reaction $N'$ on the wedge? Is it because the weight of the block is a component of the normal force $N$? If so, how do we know this?

I would be really, really grateful if somebody could kindly explain this in detail to me. Many thanks in anticipation.

 

[TSny]

The weight of the block, $W_B$, is the gravitational force acting on the block. It is not a force acting on the wedge. It is a mysterious "action-at-a-distance" force exerted by the Earth on the block.

The only force that the block exerts on the wedge is the contact force, $N$. (The gravitational attraction between the wedge and block is of course negligible.)

The value of $N$ does depend on the weight of the block as you found when you determined $N = 3mg\sin \theta$.

 

[Better WOrld]

The weight of the block, $W_B$, is the gravitational force acting on the block. It is not a force acting on the wedge. It is a mysterious "action-at-a-distance" force exerted by the Earth on the block.

The only force that the block exerts on the wedge is the contact force, $N$. (The gravitational attraction between the wedge and block is of course negligible.)

The value of $N$ does depend on the weight of the block as you found when you determined $N = 3mg\sin \theta$.

Thanks for your response.
But then when we have a block at rest on a rough inclined plane, why s the normal reaction on the wedge by the Earth equal to $W_B+W_W$?

 

[TSny]

Thanks for your response.
But then when we have a block at rest on a rough inclined plane, why s the normal reaction on the wedge by the Earth equal to $W_B+W_W$?

To see why, you'll need a good free body diagram of the block as well as the wedge. Can you describe what each diagram looks like?

 

[Better WOrld]

To see why, you'll need a good free body diagram of the block as well as the wedge. Can you describe what each diagram looks like?

Well, there would be 2 forces acting on the block: one perpendicular to the plane of the block - the normal force, and one up the surface of the inclined plane to counterbalance friction.

However, I cannot think of the FBD of the wedge. I know that the direction of the frictional force on the block and the normal force on the block will be reversed respectively. I don't know whether to include gravitational force on the block exerted on the wedge or not. Nor can I understand whether or not to include it.

 

[TSny]

Well, there would be 2 forces acting on the block: one perpendicular to the plane of the block - the normal force, and one up the surface of the inclined plane to counterbalance friction.

You have left out a force on the block. Also, I'm not sure what you mean by "to counterbalance friction". The force on the block that acts parallel to the incline is the friction force that the wedge exerts on the block. This friction force prevents the block from sliding down the incline.

However, I cannot think of the FBD of the wedge. I know that the direction of the frictional force on the block and the normal force on the block will be reversed respectively.

OK, they will be reversed (3rd law). There are two other forces that act on the wedge (but neither of these two other forces is $W_B$.)

I don't know whether to include gravitational force on the block exerted on the wedge or not. Nor can I understand whether or not to include it.

There is no such thing as "a gravitational force on the block exerted on the wedge". The gravitational force $W_B$ that acts on the block is not a force that acts on the wedge. The only forces that the block exerts on the wedge are the normal force and the friction force. $W_B$ does not act on the wedge, it acts on the block.